《2025年本土假期作业巩固训练八年级数学北师大版》

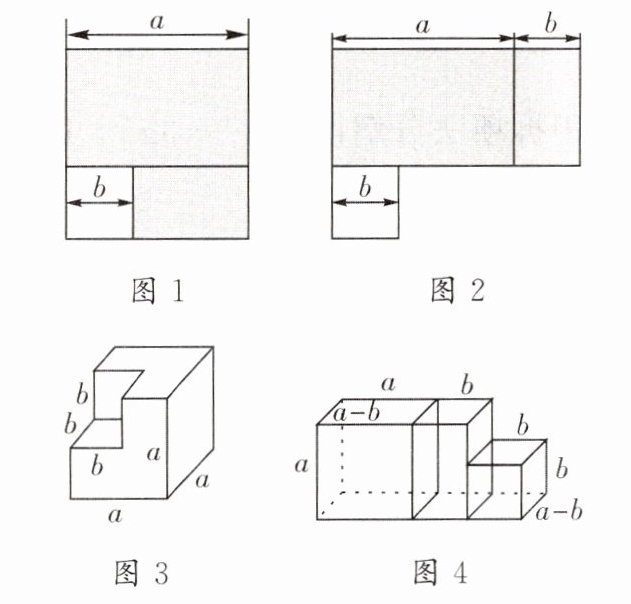
17. 【知识再现】(1) 在研究平方差公式时, 我们在边长为 $ a $ 的正方形中剪掉一个边长为 $ b $ 的小正方形 (如图 1), 把余下的阴影部分再剪拼成一个长方形 (如图 2), 根据图 1、图 2 阴影部分的面积关系可以得到一个关于 $ a,b $ 的等式$a^{2}-b^{2}=(a+b)(a-b)$;
【知识迁移】(2) 如图 3, 在边长为 $ a $ 的正方体上挖去一个边长为 $ b $ 的小正方体后, 将余下的部分再切割拼成一个几何体, 如图 4. 根据它们的体积关系可以得到关于 $ a,b $ 的等式为$a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$; (结果写成整式的积的形式)
【知识运用】(3) 已知 $ a - b = 4,ab = 3 $, 求 $ a^{3}-b^{3} $ 的值.

答案： 17.
(1)$a^{2}-b^{2}=(a+b)(a-b)$
(2)$a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$
(3)解：$\because a - b=4$，$a b=3$，
$\therefore a^{2}+b^{2}=(a - b)^{2}+2 a b=16+6=22$，
$\therefore a^{3}-b^{3}=4 ×(22+3)=100$.

18. 【调查活动】小峰同学为了完成老师布置的社会活动作业: 《A 市初中生阅读水平的现状》, 随机走访了 A 市的甲、乙两所初中, 收集到如下信息:
①甲、乙两校图书室各藏书 18000 册;
②甲校比乙校人均图书册数多 2 册;
③甲校的学生人数比乙校的人数少 $ 10\% $.
【问题解决】
请你根据上述三个信息, 就甲、乙两校的“人数”或“人均图书册数”提出一个用分式方程解决的问题, 并写出解题过程.

答案： 18. 解：问题：甲、乙两校的人数各是多少？
设乙校的人数为$x$人，则根据题意可列方程
$\frac{18000}{(1 - 10 \%) x}=\frac{18000}{x}+2$，解得$x = 1000$，
经检验，$x = 1000$是原方程的解且符合题意，
$(1 - 10 \%) x=900$（人），
答：甲、乙两校的人数各是 900 人、1000 人.
（答案不唯一）