第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列命题是假命题的是(
A.有一组邻边相等的矩形是正方形
B.对角线互相垂直的平行四边形是正方形
C.对角线相等的平行四边形是矩形
D.有三个角是直角的四边形是矩形
B
)A.有一组邻边相等的矩形是正方形
B.对角线互相垂直的平行四边形是正方形
C.对角线相等的平行四边形是矩形
D.有三个角是直角的四边形是矩形
答案:
B
2. 如下图,正方形$ABCD$的边长为3,点$P为对角线AC$上任意一点,$PE\perp BC$,$PQ\perp AB$,垂足分别是$E$,$Q$,则$PE + PQ$的值是(

A.$3\sqrt{2}$
B.3
C.$\frac{3\sqrt{2}}{2}$
D.$\frac{3}{2}$
B
)
A.$3\sqrt{2}$
B.3
C.$\frac{3\sqrt{2}}{2}$
D.$\frac{3}{2}$
答案:
B
3. 将三个大小不同的正方形如下图放置,顶点处两两相接,若正方形$A$的边长为4,正方形$C$的边长为3,则正方形$B$的面积为(
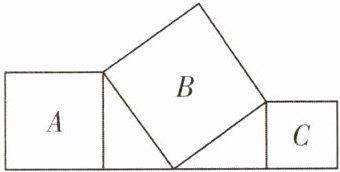
A.25
B.5
C.16
D.12
A
)
A.25
B.5
C.16
D.12
答案:
A
4. 如下图,在正方形$ABCD$中,$AB = 6$,点$Q是AB$边上的一个动点(点$Q不与点B$重合),点$M$,$N分别是DQ$,$BQ$的中点,则线段$MN$的长为(
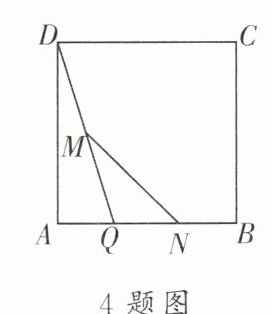
A.$3\sqrt{2}$
B.$\frac{3\sqrt{2}}{2}$
C.3
D.6
A
)
A.$3\sqrt{2}$
B.$\frac{3\sqrt{2}}{2}$
C.3
D.6
答案:
A
5. 如上图,点$E在正方形ABCD$外,连接$AE$,$BE$,$DE$,过点$A作AE$的垂线,交$DE于点F$. 若$AE = AF = \sqrt{2}$,$BF = \sqrt{10}$. 则下列结论不正确的是(
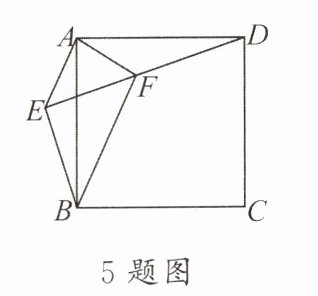
A.$\triangle AFD\cong\triangle AEB$
B.点$B到直线AE$的距离为2
C.$EB\perp ED$
D.$S_{\triangle AFD} + S_{\triangle AFB} = 1 + \sqrt{6}$
B
)
A.$\triangle AFD\cong\triangle AEB$
B.点$B到直线AE$的距离为2
C.$EB\perp ED$
D.$S_{\triangle AFD} + S_{\triangle AFB} = 1 + \sqrt{6}$
答案:
B
6. 如下图,正方形$ABCD$的边长为4,点$O$是正方形的中心,过点$O作一条直线l$,分别交正方形$AD$,$BC两边于点E$,$F$,直线$l$将正方形分成两部分,将其中一部分沿这条直线翻折到另一部分上,若$AE = 4 - 2\sqrt{2}$,求翻折后两部分图形中不重叠部分的面积.
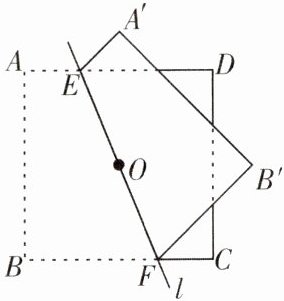

答案:
$解:连接OB,OB'$
$由折叠的性质可得:OB=OB',BF=B'F$
$∵四边形ABCD是正方形,点O是正方形的中心$
$∴OB=\frac{1}{2}BD=2\sqrt{2}$
$∵一条直线l过点O$
$∴CF=AE=4-2\sqrt{2}$
$∴BF=2\sqrt{2}$
$∴BO=BF=OB'=B'F$
$∴四边形BFB'O是菱形$
$∴OB//B'F$
$∵∠OBC=45°$
$∴∠CFB'=45°$
$∴△CFM是等腰直角三角形$
$∴∠NMB'=∠FMC=45°$
$∴△B'MN是等腰直角三角形$
$∴AE=A'P=CF=CM=4-2\sqrt{2}$
$∴PE=FM=4\sqrt{2}-4$
$∴PD=DN=4-(4\sqrt{2}-4)-(4-2\sqrt{2})=4-2\sqrt{2}$
$∴PN=4\sqrt{2}-4$
$∴NB'=MB'=4-2\sqrt{2}$
$∴不重叠部分的面积=4×\frac{1}{2}×(4-2\sqrt{2})²=48-32\sqrt{2}$
$由折叠的性质可得:OB=OB',BF=B'F$
$∵四边形ABCD是正方形,点O是正方形的中心$
$∴OB=\frac{1}{2}BD=2\sqrt{2}$
$∵一条直线l过点O$
$∴CF=AE=4-2\sqrt{2}$
$∴BF=2\sqrt{2}$
$∴BO=BF=OB'=B'F$
$∴四边形BFB'O是菱形$
$∴OB//B'F$
$∵∠OBC=45°$
$∴∠CFB'=45°$
$∴△CFM是等腰直角三角形$
$∴∠NMB'=∠FMC=45°$
$∴△B'MN是等腰直角三角形$
$∴AE=A'P=CF=CM=4-2\sqrt{2}$
$∴PE=FM=4\sqrt{2}-4$
$∴PD=DN=4-(4\sqrt{2}-4)-(4-2\sqrt{2})=4-2\sqrt{2}$
$∴PN=4\sqrt{2}-4$
$∴NB'=MB'=4-2\sqrt{2}$
$∴不重叠部分的面积=4×\frac{1}{2}×(4-2\sqrt{2})²=48-32\sqrt{2}$
查看更多完整答案,请扫码查看


