第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例 1 如下图,把一张长方形纸片 $ABCD$ 沿 $EF$ 折叠后,点 $C$,$D$ 分别落在 $C'$,$D'$ 的位置上,$ED'$ 的延长线与 $BC$ 的交点为 $G$,若 $\angle EFG = 50^{\circ}$,那么 $\angle 1$ 的度数为(
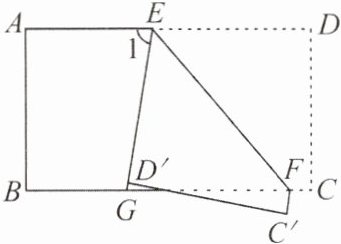
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
D
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
D
例 2 在一个正方体的每个面上都有一个汉字,其表面展开图如下图所示,那么在该正方体中,与“毒”字所在面相对的面上的字是

防
。
答案:
防
例 3 如图,$\angle ABC$ 和 $\angle BCD$ 的平分线交于点 $P$,延长 $CP$ 交 $AB$ 于点 $Q$,且 $\angle PBC + \angle PCB = 90^{\circ}$。
(1) 求证:$AB// CD$;
(2) 探究 $\angle PBC$ 与 $\angle PQB$ 的数量关系。
【思路点拨】(1) 根据角平分线的定义和平行线的判定解答即可;(2) 根据角平分线的定义解答即可。
(1) 求证:$AB// CD$;
(2) 探究 $\angle PBC$ 与 $\angle PQB$ 的数量关系。
【思路点拨】(1) 根据角平分线的定义和平行线的判定解答即可;(2) 根据角平分线的定义解答即可。
答案:
(1)证明:
∵BP平分∠ABC,
∴∠ABC=2∠PBC.
∵CP平分∠BCD,
∴∠BCD=2∠PCB,
∴∠ABC+∠BCD=2∠PBC+2∠PCB,
又
∵∠PBC+∠PCB=90°,
∴∠ABC+∠BCD=180°,
∴AB//CD.
(2)解:
∵CP平分∠DCB,
∴∠PCD=∠PCB.
∵AB//CD,
∴∠PCD=∠PQB,
∴∠PCB=∠PQB.
又
∵∠PBC+∠PCB=90°,
∴∠PBC+∠PQB=90°.
(1)证明:
∵BP平分∠ABC,
∴∠ABC=2∠PBC.
∵CP平分∠BCD,
∴∠BCD=2∠PCB,
∴∠ABC+∠BCD=2∠PBC+2∠PCB,
又
∵∠PBC+∠PCB=90°,
∴∠ABC+∠BCD=180°,
∴AB//CD.
(2)解:
∵CP平分∠DCB,
∴∠PCD=∠PCB.
∵AB//CD,
∴∠PCD=∠PQB,
∴∠PCB=∠PQB.
又
∵∠PBC+∠PCB=90°,
∴∠PBC+∠PQB=90°.
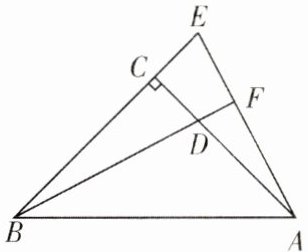
例 4 如下图,在 $Rt\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$CA = CB$,$D$ 是 $AC$ 上一点,点 $E$ 在 $BC$ 的延长线上,且 $AE = BD$,$BD$ 的延长线交 $AE$ 于点 $F$。$BD$ 与 $AE$ 有什么样的位置关系?请说明理由。
【思路点拨】先利用“HL”证明 $\triangle BDC≌\triangle AEC$,得出 $\angle CBD = \angle CAE$,从而得出 $\angle BFE = 90^{\circ}$,即 $BF⊥AE$。
【思路点拨】先利用“HL”证明 $\triangle BDC≌\triangle AEC$,得出 $\angle CBD = \angle CAE$,从而得出 $\angle BFE = 90^{\circ}$,即 $BF⊥AE$。

答案:
解:BD⊥AE,理由如下:
∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
∵BC=AC,BD=AE,
∴Rt△BDC≌Rt△AEC(HL),
∴∠CBD=∠CAE.
∵∠CAE+∠E=90°,
∴∠CBD+∠E=90°,
∴∠BFE=90°,
即BD⊥AE.
∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
∵BC=AC,BD=AE,
∴Rt△BDC≌Rt△AEC(HL),
∴∠CBD=∠CAE.
∵∠CAE+∠E=90°,
∴∠CBD+∠E=90°,
∴∠BFE=90°,
即BD⊥AE.
查看更多完整答案,请扫码查看


