第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
18. 如下图,在等边 $\triangle ABC$ 的顶点 $A$,$C$ 处各有一只蜗牛,它们同时出发,分别以相同的速度由 $A$ 向 $B$ 和由 $C$ 向 $A$ 爬行,经过 7 分钟后,它们分别爬行到 $D$,$E$ 处,设 $DC$ 与 $BE$ 的交点为 $F$。
(1) 求证:$\triangle ACD≌\triangle CBE$;
(2) 蜗牛在爬行过程中,$DC$ 与 $BE$ 所成的 $\angle BFC$ 的大小有无变化?请证明你的结论。
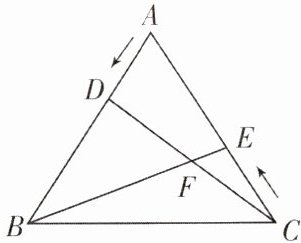
(1) 求证:$\triangle ACD≌\triangle CBE$;
(2) 蜗牛在爬行过程中,$DC$ 与 $BE$ 所成的 $\angle BFC$ 的大小有无变化?请证明你的结论。

答案:
(1)证明:
∵△ABC是等边三角形,
∴AC=CB,∠A=∠BCE=60°。
∵两只蜗牛速度相同且同时出发,
∴AD=CE。
在△ACD和△CBE中,
$\begin{cases} AC=CB \\ ∠A=∠BCE \\ AD=CE \end{cases}$,
∴△ACD≌△CBE(SAS)。
(2)解:∠BFC的大小不变。
证明:
∵△ACD≌△CBE,
∴∠ACD=∠CBE。
∵∠BFC=180°-∠FBC-∠BCD,
又
∵∠FBC=∠ACD,
∴∠BFC=180°-∠ACD-∠BCD=180°-∠ACB。
∵∠ACB=60°,
∴∠BFC=180°-60°=120°。
故∠BFC的大小不变,始终为120°。
(1)证明:
∵△ABC是等边三角形,
∴AC=CB,∠A=∠BCE=60°。
∵两只蜗牛速度相同且同时出发,
∴AD=CE。
在△ACD和△CBE中,
$\begin{cases} AC=CB \\ ∠A=∠BCE \\ AD=CE \end{cases}$,
∴△ACD≌△CBE(SAS)。
(2)解:∠BFC的大小不变。
证明:
∵△ACD≌△CBE,
∴∠ACD=∠CBE。
∵∠BFC=180°-∠FBC-∠BCD,
又
∵∠FBC=∠ACD,
∴∠BFC=180°-∠ACD-∠BCD=180°-∠ACB。
∵∠ACB=60°,
∴∠BFC=180°-60°=120°。
故∠BFC的大小不变,始终为120°。
19. 如下图,已知 $\triangle ABC$ 中,$AB = AC$,$\angle A = 108^{\circ}$,$BD$ 平分 $\angle ABC$,求证:$BC = AC + CD$。


答案:
证明:在线段BC上截取BE=BA,连接DE.
∵BD平分∠ABC,
∴∠ABD=∠EBD=$\frac{1}{2}$∠ABC.
在△ABD和△EBD中,
$\begin{cases}BA = BE\\∠ABD = ∠EBD\\BD = BD\end{cases}$,
∴△ABD≌△EBD(SAS).
∴∠BED=∠A=108°,∠ADB=∠EDB.
∵AB=AC,∠A=108°,
∴∠ACB=∠ABC=$\frac{1}{2}$×(180°−108°)=36°.
∴∠ABD=∠EBD=18°.
∴∠ADB=∠EDB=180°−∠A−∠ABD=180°−108°−18°=54°.
∴∠CDE=180°−∠ADB−∠EDB=180°−54°−54°=72°.
∠DEC=180°−∠BED=180°−108°=72°.
∴∠CDE=∠DEC.
∴CD=CE.
∵BC=BE+EC,BE=AB=AC,
∴BC=AC+CD.
∵BD平分∠ABC,
∴∠ABD=∠EBD=$\frac{1}{2}$∠ABC.
在△ABD和△EBD中,
$\begin{cases}BA = BE\\∠ABD = ∠EBD\\BD = BD\end{cases}$,
∴△ABD≌△EBD(SAS).
∴∠BED=∠A=108°,∠ADB=∠EDB.
∵AB=AC,∠A=108°,
∴∠ACB=∠ABC=$\frac{1}{2}$×(180°−108°)=36°.
∴∠ABD=∠EBD=18°.
∴∠ADB=∠EDB=180°−∠A−∠ABD=180°−108°−18°=54°.
∴∠CDE=180°−∠ADB−∠EDB=180°−54°−54°=72°.
∠DEC=180°−∠BED=180°−108°=72°.
∴∠CDE=∠DEC.
∴CD=CE.
∵BC=BE+EC,BE=AB=AC,
∴BC=AC+CD.
20. (1) 如图 1,在直线 $AB$ 上,点 $P$ 在 $A$,$B$ 两点之间,点 $M$ 为线段 $PB$ 的中点,点 $N$ 为线段 $AP$ 的中点,若 $AB = n$,且 $n$ 使关于 $x$ 的方程 $(n - 4)x = 6 - n$ 无解。
① 求线段 $AB$ 的长;
② 线段 $MN$ 的长与点 $P$ 在线段 $AB$ 上的位置有关吗?请说明理由。
(2) 如图 2,点 $C$ 为线段 $AB$ 的中点,点 $P$ 在线段 $CB$ 的延长线上,试说明 $\frac{PA + PB}{PC}$ 的值不变。
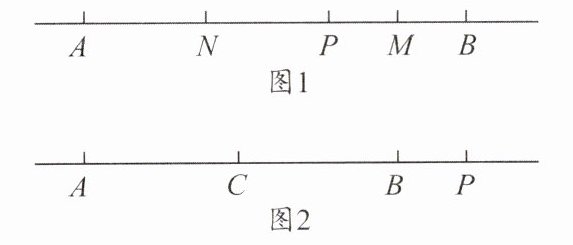
① 求线段 $AB$ 的长;
② 线段 $MN$ 的长与点 $P$ 在线段 $AB$ 上的位置有关吗?请说明理由。
(2) 如图 2,点 $C$ 为线段 $AB$ 的中点,点 $P$ 在线段 $CB$ 的延长线上,试说明 $\frac{PA + PB}{PC}$ 的值不变。

答案:
(1)①解:
∵关于$x$的方程$(n - 4)x = 6 - n$无解,
∴$n - 4 = 0$,
解得$n = 4$,
∴线段$AB$的长为$4$。
②解:无关,理由如下:
∵点$M$为线段$PB$的中点,点$N$为线段$AP$的中点,
∴$PM = \frac{1}{2}BP$,$PN = \frac{1}{2}AP$,
∵$MN = PM + PN$,
∴$MN = \frac{1}{2}BP + \frac{1}{2}AP = \frac{1}{2}(BP + AP) = \frac{1}{2}AB$,
∵$AB$的长为$4$,
∴$MN = \frac{1}{2}×4 = 2$,与点$P$的位置无关。
(2)证明:
∵点$C$为线段$AB$的中点,
∴$AC = BC = \frac{1}{2}AB$,
∵点$P$在线段$CB$的延长线上,
∴$PA = PC - AC$,$PB = PC - BC$,
∵$AC = BC$,
∴$PA + PB = (PC - AC) + (PC - BC) = 2PC - (AC + BC) = 2PC - AB$,
又
∵$AB = 2BC$,$PC = BC + BP$,
但$PA + PB = (AC + CP) + (PC - BC) = CP + AC + PC - BC$,
∵$AC = BC$,
∴$PA + PB = 2PC$,
∴$\frac{PA + PB}{PC} = \frac{2PC}{PC} = 2$,
∴$\frac{PA + PB}{PC}$的值不变,为$2$。
(1)①解:
∵关于$x$的方程$(n - 4)x = 6 - n$无解,
∴$n - 4 = 0$,
解得$n = 4$,
∴线段$AB$的长为$4$。
②解:无关,理由如下:
∵点$M$为线段$PB$的中点,点$N$为线段$AP$的中点,
∴$PM = \frac{1}{2}BP$,$PN = \frac{1}{2}AP$,
∵$MN = PM + PN$,
∴$MN = \frac{1}{2}BP + \frac{1}{2}AP = \frac{1}{2}(BP + AP) = \frac{1}{2}AB$,
∵$AB$的长为$4$,
∴$MN = \frac{1}{2}×4 = 2$,与点$P$的位置无关。
(2)证明:
∵点$C$为线段$AB$的中点,
∴$AC = BC = \frac{1}{2}AB$,
∵点$P$在线段$CB$的延长线上,
∴$PA = PC - AC$,$PB = PC - BC$,
∵$AC = BC$,
∴$PA + PB = (PC - AC) + (PC - BC) = 2PC - (AC + BC) = 2PC - AB$,
又
∵$AB = 2BC$,$PC = BC + BP$,
但$PA + PB = (AC + CP) + (PC - BC) = CP + AC + PC - BC$,
∵$AC = BC$,
∴$PA + PB = 2PC$,
∴$\frac{PA + PB}{PC} = \frac{2PC}{PC} = 2$,
∴$\frac{PA + PB}{PC}$的值不变,为$2$。
查看更多完整答案,请扫码查看


