《2025年本土假期作业巩固训练八年级数学北师大版》

知识清单
1. 三角形的中位线的定义：连接三角形两边中点的线段叫做三角形的中位线.
2. 中位线的性质：三角形的中位线平行于第三边,且等于第三边的一半.

答案： 2.平行于　第三边的一半

例1 如下图,在$\triangle ABC$中,$D$,$E$,$F分别是边BC$,$CA$,$AB$的中点. 已知$AB = 4$,$BC = 5$,$AC = 6$,则四边形$AFDE$的周长为(C)

A.$\frac{15}{2}$
B.9
C.10
D.11

答案： C

例2 如下图,在四边形$ABCD$中,对角线$AC = BD$,$E$,$F为AB$,$CD$的中点,连接$EF$,交$BD$,$AC于点P$,$Q$. 求证：$OP = OQ$.
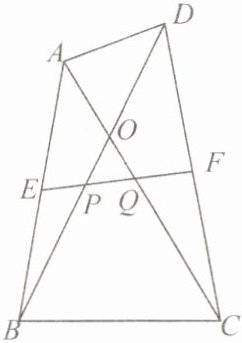
【思路点拨】取$BC的中点G$,连接$EG$,$FG$,由中位线的性质可知$EG\equalparallel\frac{1}{2}AC$,$FG\equalparallel\frac{1}{2}BD$,推出$\angle GEF = \angle AQP = \angle GFE = \angle OPQ$即可.

答案：
证明: 取BC的中点G, 连接EG, FG, 如右图,
∵E,G为AB,BC的中点,
∴EG = $\frac{1}{2}$AC, EG//AC,

∴∠FEG = ∠OQP,
同理, FG = $\frac{1}{2}$BD, FG//BD,
∴∠EFG = ∠OPQ,
∵AC = BD,
∴EG = FG,
∴∠FEG = ∠EFG,
∴∠OPQ = ∠OQP,
∴OP = OQ.

1. 如下图,在四边形$ABCD$中,$AD = BC$,$E$,$F$,$G分别是AB$,$CD$,$AC$的中点,则下列结论错误的是(B)

A.$GF = \frac{1}{2}AD$
B.$EF = \frac{1}{2}AC$
C.$GE = \frac{1}{2}BC$
D.$GE = GF$

答案： B

2. 如下图,要测量被池塘隔开的$A$,$B$两点的距离,小明在$AB外选一点C$,连接$AC$,$BC$,并分别找出它们的中点$M$,$N$,连接$MN$,现测得$MN = 45$米,那么$AB = $90米.

答案： 90

3. 如下图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$D为\triangle ABC$外一点,使$\angle DAC = \angle BAC$,$E为BD$的中点,$\angle ABC = 50^{\circ}$,求$\angle ACE$的度数.

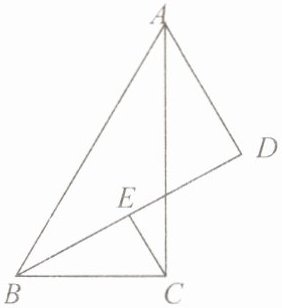
答案： 1. 首先，在$Rt\triangle ABC$中：
已知$\angle ACB = 90^{\circ}$，$\angle ABC = 50^{\circ}$，根据三角形内角和公式$\angle A+\angle B+\angle C = 180^{\circ}$，可得$\angle BAC=180^{\circ}-\angle ACB - \angle ABC$。
把$\angle ACB = 90^{\circ}$，$\angle ABC = 50^{\circ}$代入，得$\angle BAC = 40^{\circ}$。
因为$\angle DAC=\angle BAC$，所以$\angle DAC = 40^{\circ}$，则$\angle BAD=\angle BAC+\angle DAC=80^{\circ}$。
2. 然后，延长$CE$交$AB$于点$F$：
因为$E$为$BD$的中点，$\angle BEC=\angle DEA$（对顶角相等），$\angle EBF=\angle EDA$（两直线平行，内错角相等，这里可通过构造全等三角形的思路，$\triangle BEF\cong\triangle DEC$（$AAS$：$\angle BEF=\angle DEC$，$BE = DE$，$\angle EBF=\angle EDC$）），所以$CE = FE$。
在$\triangle ACF$中，$CE = FE$，$AC$是公共边，$\angle FAC=\angle DAC$，$AE = AE$（这里可利用全等三角形判定$SAS$），$\triangle ACF$是等腰三角形（$AC$为角平分线，$CE = FE$，根据等腰三角形三线合一的逆定理）。
又因为$\angle ACB = 90^{\circ}$，$CE$是$Rt\triangle ACF$斜边$AF$上的中线。
3. 最后，求$\angle ACE$的度数：
根据直角三角形斜边中线定理，$CE = AE$，所以$\angle ACE=\angle CAE$。
已知$\angle BAC = 40^{\circ}$，$\angle DAC=\angle BAC$，$\angle ACE=\frac{1}{2}(180^{\circ}-\angle BAD)$（因为$\angle BAD = 80^{\circ}$，且$\triangle ACF$中$AC$平分$\angle BAD$，$CE$是中线也是角平分线）。
把$\angle BAD = 80^{\circ}$代入，得$\angle ACE = 40^{\circ}$。
所以$\angle ACE$的度数为$40^{\circ}$。