《2025年本土假期作业巩固训练八年级数学北师大版》

知识清单
1. $n$边形的内角和等于(n - 2)·180°.
2. $n$边形的外角和等于360°.
3. $n$边形共有$\frac{1}{2}$n(n - 3)条对角线.

答案： 1. (n - 2)·180°
2. 360°
3. $\frac{1}{2}$n(n - 3)

例1 若正多边形的一个外角是$60^{\circ}$,则该正多边形的内角和为(C)
A.$360^{\circ}$
B.$540^{\circ}$
C.$720^{\circ}$
D.$900^{\circ}$

答案： C

1. 一个多边形的每个内角都相等,每个内角与相邻外角的差为$100^{\circ}$,求这个多边形内角和的度数和边数.

答案： 解：设这个多边形的每个外角为$x^{\circ}$，则每个内角为$(x + 100)^{\circ}$。
因为多边形的内角与相邻外角互补，所以$x + (x + 100) = 180$，
解得$x = 40$。
因为多边形的外角和为$360^{\circ}$，所以边数$n = 360÷40 = 9$。
内角和度数为$(9 - 2)×180^{\circ} = 1260^{\circ}$。
答：这个多边形内角和的度数为$1260^{\circ}$，边数为$9$。

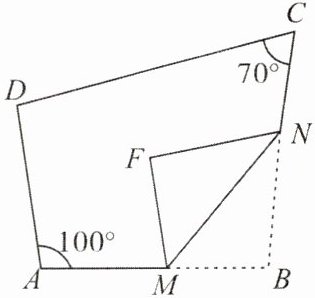
2. 如下图,在四边形$ABCD$中,$\angle BAD = 100^{\circ}$,$\angle BCD = 70^{\circ}$,点$M$,$N分别在AB$,$BC$上,将$\triangle BMN沿MN$翻折,得$\triangle FMN$,若$MF// AD$,$FN// DC$,求$\angle B$的度数.

答案： 解：
∵MF//AD，∠BAD=100°，
∴∠BMF=∠BAD=100°，
∵△BMN沿MN翻折得△FMN，
∴∠BMN=∠FMN，
∴∠BMN=∠FMN=∠BMF/2=50°，
∵FN//DC，∠BCD=70°，
∴∠BNF=∠BCD=70°，
∵△BMN沿MN翻折得△FMN，
∴∠BNM=∠FNM，
∴∠BNM=∠FNM=∠BNF/2=35°，
在△BMN中，∠B=180°-∠BMN-∠BNM=180°-50°-35°=95°。
答：∠B的度数为95°。

知识清单
1. 菱形的概念
一组邻边相等的平行四边形是菱形.
2. 菱形的性质
(1) 菱形是特殊的平行四边形,具有平行四边形的所有性质.
(2) 菱形的四条边相等.
(3) 菱形的对角线互相垂直,并且每一条对角线平分一组对角.
3. 菱形的判定
(1) 一组邻边相等的平行四边形是菱形.
(2) 对角线互相垂直平分的四边形是菱形.
(3) 四条边都相等的四边形是菱形.

答案： 1. 相等
2.
(2)相等　
(3)互相垂直
3.
(1)相等　
(2)互相垂直平分

例1 如下图,在菱形$ABCD$中,点$E$,$F分别是AC$,$DC$的中点. 若$EF = 3$,则菱形$ABCD$的周长为(D)

A.12
B.16
C.20
D.24

答案： D

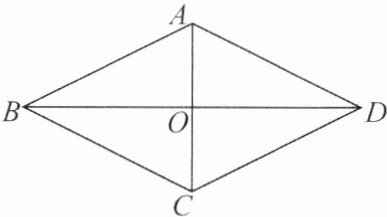
例2 如下图,在四边形$ABCD$中,$AB = AD$,$BD平分\angle ABC$,$AC\perp BD$,垂足为$O$.
(1) 求证：四边形$ABCD$是菱形；
(2) 若$CD = 3$,$BD = 2\sqrt{5}$,求四边形$ABCD$的面积.
【思路点拨】(1) 根据等腰三角形的性质得到$\angle ABD = \angle ADB$,根据角平分线的定义得到$\angle ABD = \angle CBD$,等量代换得到$\angle ADB = \angle CBD$,根据全等三角形的性质得到$AO = OC$,于是得到结论；(2) 根据菱形的性质得到$OD = \frac{1}{2}BD = \sqrt{5}$,根据勾股定理得到$OC = \sqrt{CD^{2} - OD^{2}} = 2$,于是得到结论.

答案： 1. 证明四边形$ABCD$是菱形：
解：
因为$AB = AD$，所以$\angle ABD=\angle ADB$。
因为$BD$平分$\angle ABC$，所以$\angle ABD = \angle CBD$。
则$\angle ADB=\angle CBD$。
又因为$AC\perp BD$，$AB = AD$，所以$BO = OD$（等腰三角形三线合一）。
在$\triangle AOD$和$\triangle COB$中，$\left\{\begin{array}{l}\angle AOD=\angle COB\\OD = OB\\\angle ADO=\angle CBO\end{array}\right.$，根据$ASA$（角 - 边 - 角）可得$\triangle AOD\cong\triangle COB$。
所以$AO = OC$。
因为$AC\perp BD$，$AO = OC$，$BO = OD$，所以四边形$ABCD$是菱形（对角线互相垂直且平分的四边形是菱形）。
2. 求四边形$ABCD$的面积：
解：
因为四边形$ABCD$是菱形，所以$OD=\frac{1}{2}BD$，已知$BD = 2\sqrt{5}$，则$OD=\sqrt{5}$。
又因为$CD = 3$，$AC\perp BD$，在$Rt\triangle COD$中，根据勾股定理$a^{2}+b^{2}=c^{2}$（这里$c = CD$，$a = OD$，$b = OC$），可得$OC=\sqrt{CD^{2}-OD^{2}}$。
把$CD = 3$，$OD=\sqrt{5}$代入$OC=\sqrt{CD^{2}-OD^{2}}$，得$OC=\sqrt{3^{2}-\left(\sqrt{5}\right)^{2}}=\sqrt{9 - 5}=\sqrt{4}=2$。
所以$AC=2OC = 4$。
根据菱形面积公式$S=\frac{1}{2}AC\cdot BD$，把$AC = 4$，$BD = 2\sqrt{5}$代入可得$S=\frac{1}{2}×4×2\sqrt{5}=4\sqrt{5}$。
综上，（1）四边形$ABCD$是菱形得证；（2）四边形$ABCD$的面积是$4\sqrt{5}$。