《2025年本土假期作业巩固训练八年级数学北师大版》

8. 嘉琪要比较 $ \sqrt { 5 } + 1 $ 与 $ \sqrt { 10 } $ 的大小,步骤如下.
① 如图,构造 $ \mathrm { Rt } \triangle A B C $,其中 $ A B = 1 $,$ \angle B = 90 ^ { \circ } $,若要使 $ A C = \sqrt { 10 } $,则 $ B C = $3；
② 在边 $ B C $ 上取 $ C D = 1 $,连接 $ A D $,则 $ A D = $$\sqrt{5}$；
③ 在 $ \triangle A D C $ 中,利用三角形的三边关系可得 $ A D + C D ＞ A C $,即 $ \sqrt { 5 } + 1 ＞ \sqrt { 10 } $.

答案： ①3 ②$\sqrt{5}$

9. 如图,点 $ D $,$ E $ 都在 $ \triangle A B C $ 的边上,$ D E // B C $,$ \angle A B C $ 和 $ \angle A C B $ 的平分线分别交 $ D E $ 于 $ G $,$ F $ 两点. 若 $ B E + C D = 25 $,则 $ D E - F G $ 的值为______25.

答案： 25

10. 将点 $ P ( m + 2,2 m + 4 ) $ 向左平移 1 个单位长度得到点 $ P ^ { \prime } $,且点 $ P ^ { \prime } $ 在 $ y $ 轴上,则点 $ P ^ { \prime } $ 的坐标是______(0,2).

答案： $(0,2)$

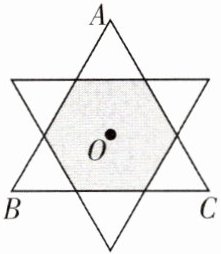
11. 如图,将边长为 $ 3 \mathrm { cm } $ 的正三角形 $ A B C $ 绕它的中心 $ O $ 旋转 $ 60 ^ { \circ } $,则图中阴影部分的面积为$\frac{3\sqrt{3}}{2}$$ \mathrm { cm } ^ { 2 } $.

答案： $\frac{3\sqrt{3}}{2}$

12. 如图,方格图中每个小正方形的边长都为 1.
(1)填空：$ B C = $______$2\sqrt{5}$,$ A B = $______$\sqrt{26}$；
(2)若连接 $ C D $,$ \angle B C D $ 是直角吗？如果是,请予以证明；如果不是,请说明理由；
(3)求点 $ D $ 到 $ A B $ 的距离.

答案：
(1)$2\sqrt{5}$；$\sqrt{26}$
(2)解：$∠BCD$是直角，证明如下：由题意，得$CD=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$BD=\sqrt{3^{2}+4^{2}}=5$，$\because CD^{2}+BC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=25=5^{2}=BD^{2}$，$\therefore \triangle BCD$是直角三角形，即$∠BCD=90^{\circ}$，$\therefore ∠BCD$是直角.
(3)解：设点$D$到$AB$的距离为$h$，由题意，得$S_{\triangle ABD}=5×4-\frac{1}{2}×1×4-\frac{1}{2}×3×4-\frac{1}{2}×1×5=\frac{19}{2}$，$\therefore \frac{1}{2}AB\cdot h=\frac{19}{2}$，用$\frac{1}{2}\cdot \sqrt{26}h=\frac{19}{2}$，解得$h=\frac{19\sqrt{26}}{26}$.$\therefore$点$D$到$AB$的距离为$\frac{19\sqrt{26}}{26}$.

13. 如图,在四边形 $ A B C D $ 中,$ A B = 2 $,$ B C = 3 $,$ C D = 2 \sqrt { 3 } $,$ A D = 5 $,$ \angle B = 90 ^ { \circ } $. 求四边形 $ A B C D $ 的面积.

答案：
解：连接$AC$，如图，$\because AB=2$，$BC=3$，$∠B=90^{\circ}$， $\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{13}$，$\because CD=2\sqrt{3}$，$AD=5$，$(\sqrt{13})^{2}+(2\sqrt{3})^{2}=5^{2}$，即$AC^{2}+CD^{2}=AD^{2}$，$\therefore \triangle ACD$是直角三角形，$\therefore S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}×2×3+\frac{1}{2}×\sqrt{13}×2\sqrt{3}=3+\sqrt{39}$.