《2025年本土假期作业巩固训练八年级数学北师大版》

例 1 坐标平面内一点 $M(b^{2}+1,-\sqrt{a}-3)$ 在第四象限。
【思路点拨】$\because b^{2}≥0$,$\therefore b^{2}+1＞0$,$\because \sqrt{a}≥0$,$\therefore -\sqrt{a}-3＜0$,$\therefore$ 点 $M$ 在第四象限。

答案： 四

例 2 已知点 $A(-2,y_{1})$,$B(-3,y_{2})$,$C(3,y_{3})$ 都在关于 $x$ 的一次函数 $y = -x + m$ 的图象上,则 $y_{1}$,$y_{2}$,$y_{3}$ 之间的大小关系是y₃＜y₁＜y₂。

答案： y₃＜y₁＜y₂

例 3 某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量 $y$(个)与甲车间加工时间 $t$(h)之间的函数图象如下图所示。
(1) 求乙车间加工零件的数量 $y$ 与甲车间加工时间 $t$ 之间的函数关系式,并写出 $t$ 的取值范围；
(2) 求甲车间加工的零件总量 $a$；
(3) 当甲、乙两车间加工零件总数量为 320 个时,直接写出 $t$ 的值。
【思路点拨】(1) 运用待定系数法解答即可；(2) 把已知条件代入函数的表达式即可得到结论；(3) 把 $y = 320$ 代入(1) 的结论解答即可。

答案：
(1) 设乙车间加工零件的数量 $ y $ 与甲车间加工时间 $ t $ 之间的函数关系式为 $ y=kt+b $。由图可知，乙车间从 $ t=5 $ 时开始加工，此时 $ y=0 $；当 $ t=8 $ 时，乙车间加工零件数量为 $ 120 $ 个。将 $ (5,0) $，$ (8,120) $ 代入得：$\begin{cases}5k + b = 0 \\8k + b = 120\end{cases}$，解得$\begin{cases}k = 40 \\b=-200\end{cases}$，所以函数关系式为 $ y = 40t - 200 $，$ t $ 的取值范围是 $ 5 \leq t \leq 8 $。
(2) 解：甲车间停产前 3 小时加工 120 个，工作效率为 $ 120÷3 = 40 $（个/小时）。甲车间总加工时间为 $ 8 - 1 = 7 $（小时）（其中停产 1 小时），则 $ a = 40×7 = 280 $。
(3) 解：当 $ t \leq 5 $ 时，乙未开始加工，甲加工数量为 $ 40t $（$ t \leq 3 $）或 $ 120 $（$ 3 ＜ t \leq 4 $）或 $ 120 + 40(t - 4) $（$ 4 ＜ t ＜ 5 $），此时总数量不可能为 320。当 $ 5 \leq t \leq 8 $ 时，甲加工数量为 $ 120 + 40(t - 4) $，乙加工数量为 $ 40t - 200 $，总数量为 $ 120 + 40(t - 4) + 40t - 200 = 320 $，解得 $ t = 6 $。即 $ t = 6 $。

1. 在平面直角坐标系中,点 $A(1,-2)$ 关于 $x$ 轴对称的点的坐标是(B)
A.$(1,-2)$
B.$(1,2)$
C.$(-1,2)$
D.$(-1,-2)$

答案： B

2. 在平面直角坐标系中,若点 $A(2,a)$ 在第四象限内,则点 $B(a,2)$ 所在的象限是(B)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： B

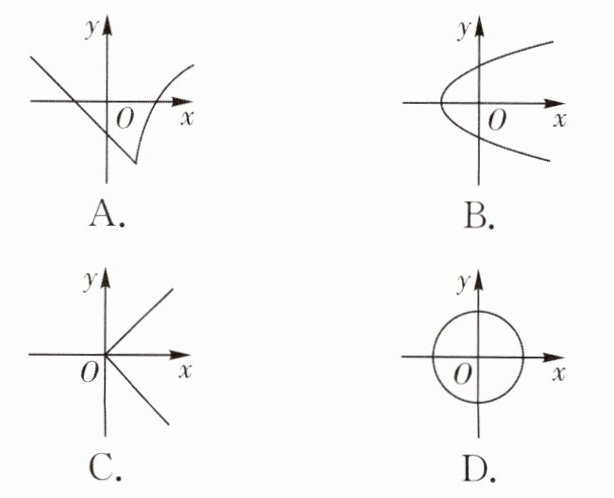
3. 下列图象中,表示 $y$ 是 $x$ 的函数的是(A)

答案： A