《2025年本土假期作业巩固训练八年级数学北师大版》

11. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如下图是一个正方体的平面展开图,若图中的“方”表示正方体的前面,“法”表示右面,“想”表示下面,则“数”“学”“思”分别表示正方体的后面、上面、左面。

答案： 后面、上面、左面

12. 如下图,已知 $AB// CD$,则 $\angle A$,$\angle C$,$\angle P$ 的关系为∠A+∠C−∠P=180°。

答案： ∠A+∠C−∠P=180°

13. 如上图,$BA⊥AC$,$CD// AB$,$BC = DE$,且 $BC⊥DE$,已知 $AB = 5$,$CD = 8$,则 $AE$ 的长为______3。

答案： 3

14. 在平面直角坐标系中,已知点 $A$,$B$ 的坐标分别是 $(2,0)$,$(4,2)$,若在 $x$ 轴下方有一点 $P$,使以 $O$,$A$,$P$ 为顶点的三角形与 $\triangle OAB$ 全等,则满足条件的 $P$ 点的坐标是(−2,−2)或(4,−2)。

答案： (−2,−2)或(4,−2)

15. 如下图,点 $P$ 是正方形 $ABCD$ 的对角线 $BD$ 上一点,$PE⊥BC$ 于点 $E$,$PF⊥CD$ 于点 $F$,连接 $E$,$F$。给出下列五个结论：① $AP = EF$；② $PD = EC$；③ $\angle PFE = \angle BAP$；④ $\triangle APD$ 一定是等腰三角形；⑤ $AP⊥EF$。其中正确结论的序号是______①③⑤。

答案： ①③⑤

16. 如下图,$\angle ABC = \angle ADC$,$BE$,$DF$ 分别是 $\angle ABC$,$\angle ADC$ 的角平分线,且 $\angle 2 = \angle 3$,求证：$BC// AD$。

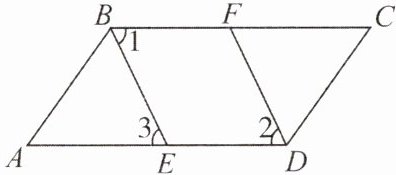
答案： 证明:
∵BE,DF分别是∠ABC和∠ADC的平分线，
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC,
∵∠ABC=∠ADC,
∴∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
∴BC//AD.

17. 如下图,$\triangle ADC$ 中,$DB$ 是高,点 $E$ 是 $DB$ 上一点,$AB = DB$,$EB = CB$,$M$,$N$ 分别是 $AE$,$CD$ 上的点,且 $AM = DN$。
(1) 求证：$\triangle ABE≌\triangle DBC$；
(2) 探索 $BM$ 和 $BN$ 的数量关系和位置关系,并证明你的结论。

答案：
(1)证明：
∵DB是高，
∴∠ABE=∠DBC=90°。
在△ABE和△DBC中，
$\begin{cases}AB = DB\\∠ABE = ∠DBC\\BE = BC\end{cases}$
∴△ABE≌△DBC(SAS)。
(2)解：BM=BN，MB⊥BN。
证明如下：
∵△ABE≌△DBC，
∴∠BAM=∠BDN。
在△ABM和△DBN中，
$\begin{cases}AB = DB\\∠BAM = ∠BDN\\AM = DN\end{cases}$
∴△ABM≌△DBN(SAS)，
∴BM=BN，∠ABM=∠DBN，
∴∠DBN+∠DBM=∠ABM+∠DBM=∠ABD=90°，
∴MB⊥BN。