第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4. 函数 $y = \frac{\sqrt{x - 1}}{2 - x}$ 中自变量 $x$ 的取值范围是(
A.$x≥1$
B.$x≠2$
C.$x>1$ 或 $x≠2$
D.$x≥1$ 且 $x≠2$
D
)A.$x≥1$
B.$x≠2$
C.$x>1$ 或 $x≠2$
D.$x≥1$ 且 $x≠2$
答案:
D
5. 已知一次函数 $y = -2x + 1$,当 $x≤0$ 时,$y$ 的取值范围为(
A.$y≤1$
B.$y≥0$
C.$y≤0$
D.$y≥1$
D
)A.$y≤1$
B.$y≥0$
C.$y≤0$
D.$y≥1$
答案:
D
6. 在平面直角坐标系中,将直线 $l_{1}:y = 3x - 2$ 向右平移 2 个单位得到直线 $l_{2}$,则要得到直线 $l_{2}$,还可以将直线 $l_{1}$(
A.向上平移 2 个单位
B.向下平移 2 个单位
C.向上平移 6 个单位
D.向下平移 6 个单位
D
)A.向上平移 2 个单位
B.向下平移 2 个单位
C.向上平移 6 个单位
D.向下平移 6 个单位
答案:
D
7. 如下图,在平面直角坐标系中,一动点从原点 $O$ 出发,按向上,向右,向下,向右……的方向不断地移动,每次移动一个单位长度,得到点 $A_{1}(0,1)$,$A_{2}(1,1)$,$A_{3}(1,0)$,$A_{4}(2,0)$,那么 $A_{2024}$ 的坐标为(
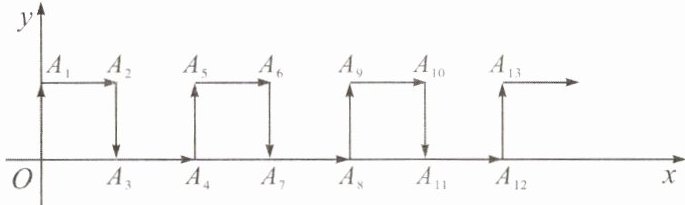
A.$(2024,1)$
B.$(2024,0)$
C.$(1012,1)$
D.$(1012,0)$
D
)
A.$(2024,1)$
B.$(2024,0)$
C.$(1012,1)$
D.$(1012,0)$
答案:
D
8. 正方形 $A_{1}B_{1}C_{1}A_{2}$,$A_{2}B_{2}C_{2}A_{3}$,$A_{3}B_{3}C_{3}A_{4}$,…,按如下图所示的方式放置,点 $A_{1}$,$A_{2}$,$A_{3}$,…和点 $B_{1}$,$B_{2}$,$B_{3}$,…分别在直线 $y = x + 1$ 和 $x$ 轴上,则点 $C_{2024}$ 的纵坐标是(

A.$2^{2023}$
B.$2^{2024}$
C.$2^{2023}-1$
D.$2^{2024}-1$
A
)
A.$2^{2023}$
B.$2^{2024}$
C.$2^{2023}-1$
D.$2^{2024}-1$
答案:
A
9. 已知点 $A(3a - 6,a + 4)$,$B(-3,2)$,$AB// y$ 轴,点 $P$ 为直线 $AB$ 上一点,且 $PA = 2PB$,则点 $P$ 的坐标为
(−3,3)或(−3,−1)
。
答案:
(−3,3)或(−3,−1)
10. 在一次函数 $y = (2a - 5)x + 1$ 中,$y$ 的值随着 $x$ 值的增大而减小,则 $a$ 的取值范围是
a<$\frac{5}{2}$
。
答案:
a<$\frac{5}{2}$
11. 碚碚用新买的 50 元 5G 电话卡打长途电话,按通话时间 3 分钟内收 1.2 元,3 分钟后每超过 1 分钟加收 0.3 元钱的方式缴纳话费。若通话时间为 $t$ 分钟($t$ 大于等于 3 分钟),那么电话费用 $w$(元)与通话时间 $t$(分钟)的关系式可以表示为
w=0.3t+0.3(t≥3)
。
答案:
w=0.3t+0.3(t≥3)
12. 一个有进水管和出水管的容器,从某时刻开始 4 min 内只进水不出水,在随后的 8 min 内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量 $y$(L)与时间 $x$(min)之间的关系如下图所示,则每分钟的出水量为
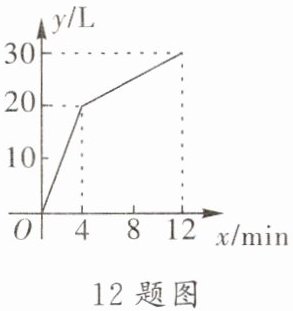
3.75
L。
答案:
3.75
13. 如上图,在直角坐标系中,直线 $y = \frac{4}{3}x + 4$ 分别交 $x$ 轴,$y$ 轴于 $A$,$B$ 两点,$C$ 为 $OB$ 的中点,点 $D$ 在第二象限,且四边形 $AOCD$ 为矩形,$P$ 是 $CD$ 上一个动点,过点 $P$ 作 $PH⊥OA$ 于点 $H$,$Q$ 是点 $B$ 关于点 $A$ 的对称点,则 $BP + PH + HQ$ 的最小值为
6$\sqrt{2}$+2
。
答案:
6$\sqrt{2}$+2
14. 如下图,已知长方形 $ABCD$ 中,$AB = CD = 16$,$BC = DA = 24$,$E$ 为 $CD$ 边的中点,$P$ 为长方形 $ABCD$ 边上的动点,动点 $P$ 以 4 个单位长度/s 的速度从 $A$ 出发,沿着 $A→B→C→E$ 运动到 $E$ 点停止,设点 $P$ 运动的时间为 $t$ s,$\triangle APE$ 的面积为 $y$。
(1) 当 $t = 2$ 时,$y$ 的值是______
(2) 在点 $P$ 运动过程中,求 $y$ 与 $t$ 之间的关系式。
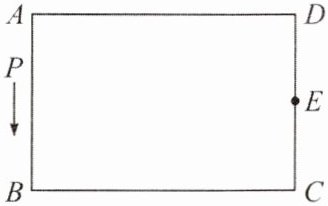
(1) 当 $t = 2$ 时,$y$ 的值是______
96
;当 $t = 6$ 时,$y$ 的值是______160
;(2) 在点 $P$ 运动过程中,求 $y$ 与 $t$ 之间的关系式。

答案:
(1)96;160
(2)解:①当P在AB上时(如答图1),即0≤t≤4时,此时,AP=4t,
∴△APE的面积为y=$\frac{1}{2}$×4t×24=48t; ②当点P在BC上时(如答图2),即4<t≤10,此时BP=4t−16,则PC=24−(4t−16)=40−4t,
∴y=24×16−$\frac{1}{2}$×16×(4t−16)−$\frac{1}{2}$×(40−4t)×8 −$\frac{1}{2}$×24×8=−16t+256,所以y与t之间的关系式为y=−16t+256; ③当点P在BC上时(如答图3),即10<t≤12,PE=48−4t,
∴△APE的面积为y=$\frac{1}{2}$(48−4t)×24=−48t+576.综上,y与t的函数关系式为$y=\begin{cases}48t(0\leq t\leq4)\\-16t + 256(4\lt t\leq10)\\-48t + 576(10\lt t\leq12)\end{cases}$
(1)96;160
(2)解:①当P在AB上时(如答图1),即0≤t≤4时,此时,AP=4t,
∴△APE的面积为y=$\frac{1}{2}$×4t×24=48t; ②当点P在BC上时(如答图2),即4<t≤10,此时BP=4t−16,则PC=24−(4t−16)=40−4t,
∴y=24×16−$\frac{1}{2}$×16×(4t−16)−$\frac{1}{2}$×(40−4t)×8 −$\frac{1}{2}$×24×8=−16t+256,所以y与t之间的关系式为y=−16t+256; ③当点P在BC上时(如答图3),即10<t≤12,PE=48−4t,
∴△APE的面积为y=$\frac{1}{2}$(48−4t)×24=−48t+576.综上,y与t的函数关系式为$y=\begin{cases}48t(0\leq t\leq4)\\-16t + 256(4\lt t\leq10)\\-48t + 576(10\lt t\leq12)\end{cases}$
查看更多完整答案,请扫码查看


