《2025年本土假期作业巩固训练八年级数学北师大版》

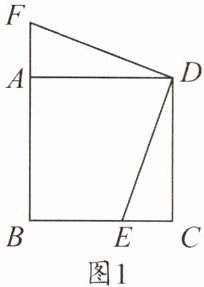
例1 如图1,$E为正方形ABCD的边BC$上一点,$F为边BA$延长线上一点,且$CE = AF$.
(1) 求证：$DE\perp DF$.

(2) 如图2,在(1)的条件下,若点$G为边AB$上一点,且$\angle BGE = 2\angle BFE$,$\triangle BGE$的周长为16,求四边形$DEBF$的面积.


(3) 如图3,在(2)的条件下,$DG与EF交于点H$,连接$CH$,若$CH = 5\sqrt{2}$,求$AG$的长.

答案： $(1)$ 证明$DE\perp DF$
解：
因为四边形$ABCD$是正方形，所以$AD = CD$，$\angle DAF=\angle DCE = 90^{\circ}$。
在$\triangle ADF$和$\triangle CDE$中，$\begin{cases}AD = CD\\\angle DAF=\angle DCE\\AF = CE\end{cases}$，根据$SAS$（边角边）定理可得$\triangle ADF\cong\triangle CDE$。
所以$\angle ADF=\angle CDE$。
因为$\angle CDE+\angle ADE = 90^{\circ}$，所以$\angle ADF+\angle ADE = 90^{\circ}$，即$\angle EDF = 90^{\circ}$，所以$DE\perp DF$。
$(2)$ 求四边形$DEBF$的面积
解：
因为$\angle BGE = 2\angle BFE$，$\angle BGE=\angle BFE+\angle FEG$，所以$\angle BFE=\angle FEG$，则$GE = GF$。
$\triangle BGE$的周长$=BE + BG+GE=BE + BG + GF=BE + BF$。
由$(1)$知$\triangle ADF\cong\triangle CDE$，所以$DF = DE$，$\angle EDF = 90^{\circ}$，四边形$DEBF$的面积$S = S_{\triangle DFE}+S_{\triangle DBE}$。
又因为$S_{\triangle ADF}=S_{\triangle CDE}$，所以四边形$DEBF$的面积$S = S_{正方形ABCD}$。
因为$\triangle BGE$的周长为$16$，即$BE + BF=16$，设正方形边长为$a$，$BF=BA + AF$，$AF = CE$，$BE + BF=(BC - CE)+(BA + AF)=2a = 16$，解得$a = 8$。
根据正方形面积公式$S=a^{2}$，所以四边形$DEBF$的面积$S = 8×8=64$。
$(3)$ 求$AG$的长
解：
$过点H作HP⊥HC交CB的延长线于点P$
$因为GF=GE,DF=DE$
$所以DG垂直平分EF$
$因为∠FDE=90°$
$所以DH=EH,∠DHE=∠PHC=90°$
$所以∠DHE-∠HEC=∠PHC-∠HEC$
$所以∠DHC=∠EHP$
$因为∠HDC+∠HEC=180°且∠HEC+∠HEP=180°$
$所以∠HEP=∠HDC$
$所以△HDC≌△HEP$
$所以DC=PE=8,HC=HP=5\sqrt{2}$
$所以PC=10$
$所以EC=PC-PE=2$
$所以AF=2,BE=6$
$设EG=x$
$则BG=10-x$
$所以(10-x)²+6²=x²$
$解得x=\frac{34}{5}$
$所以AG=GF-AF=\frac{24}{5}$