第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
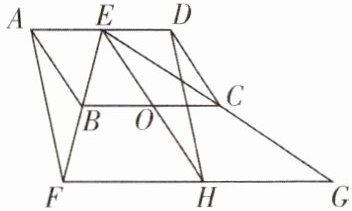
23. 如图,点$E为□ ABCD的边AD$上的一点,连接$EB$并延长,使$BF = BE$,连接$EC$并延长,使$CG = CE$,连接$FG$. $H为FG$的中点,连接$DH$,$AF$.
(1) 若$\angle BAE = 70^{\circ}$,$\angle DCE = 20^{\circ}$,求$\angle DEC$的度数;
(2) 求证:四边形$AFHD$为平行四边形;
(3) 连接$EH$,交$BC于点O$,若$OC = OH$,求证:$EF\perp EG$.
(1) 若$\angle BAE = 70^{\circ}$,$\angle DCE = 20^{\circ}$,求$\angle DEC$的度数;
(2) 求证:四边形$AFHD$为平行四边形;
(3) 连接$EH$,交$BC于点O$,若$OC = OH$,求证:$EF\perp EG$.

答案:
(1)50°
(2)证明:
∵四边形ABCD是平行四边形,
∴AD = BC, AD//BC, ∠BAE = ∠BCD,
∵BF = BE, CG = CE,
∴BC是△EFG的中位线,
∴BC//FG, BC = $\frac{1}{2}$FG, 又
∵H为FG的中点,
∴FH = $\frac{1}{2}$FG,
∴BC//FH, BC = FH,
∴AD//FH, AD = FH,
∴四边形AFHD是平行四边形.
(3)证明: 连接CH,BH如下图,
∵CE = CG, FH = HG,
∴CH = $\frac{1}{2}$EF, CH//EF,
∵EB = BF = $\frac{1}{2}$EF,
∵BE = CH,
∴四边形EBHC是平行四边形,
∴OB = OC, OE = OH,
∵OC = OH,
∴OE = OB = OC = OH,
∴四边形EBHC是矩形,
∴∠FEG = 90°,
∴EF⊥EG.

(1)50°
(2)证明:
∵四边形ABCD是平行四边形,
∴AD = BC, AD//BC, ∠BAE = ∠BCD,
∵BF = BE, CG = CE,
∴BC是△EFG的中位线,
∴BC//FG, BC = $\frac{1}{2}$FG, 又
∵H为FG的中点,
∴FH = $\frac{1}{2}$FG,
∴BC//FH, BC = FH,
∴AD//FH, AD = FH,
∴四边形AFHD是平行四边形.
(3)证明: 连接CH,BH如下图,
∵CE = CG, FH = HG,
∴CH = $\frac{1}{2}$EF, CH//EF,
∵EB = BF = $\frac{1}{2}$EF,
∵BE = CH,
∴四边形EBHC是平行四边形,
∴OB = OC, OE = OH,
∵OC = OH,
∴OE = OB = OC = OH,
∴四边形EBHC是矩形,
∴∠FEG = 90°,
∴EF⊥EG.

24. 已知点$P$,$Q分别在菱形ABCD的边BC$,$CD$上滑动(点$P不与B$,$C$两点重合),且$\angle PAQ = \angle B$.
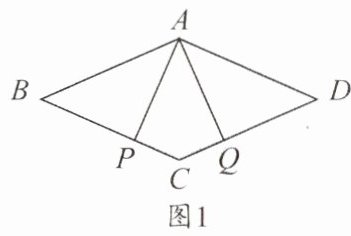
(1) 如图1,若$AP\perp BC$,求证:$AP = AQ$.
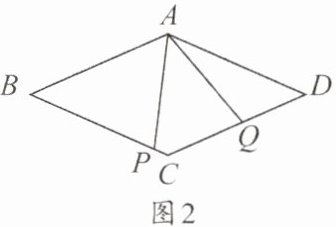
(2) 如图2,若$AP与BC$不垂直,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
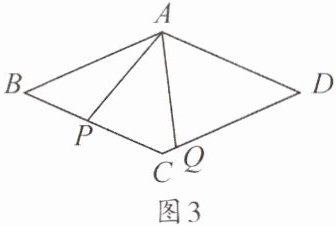
(3) 如图3,若$AB = 4$,$\angle B = 60^{\circ}$,请直接写出四边形$APCQ$的面积.
(1) 如图1,若$AP\perp BC$,求证:$AP = AQ$.
(2) 如图2,若$AP与BC$不垂直,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
(3) 如图3,若$AB = 4$,$\angle B = 60^{\circ}$,请直接写出四边形$APCQ$的面积.



答案:
$(1)$ 证明$AP = AQ$
解:
因为四边形$ABCD$是菱形,所以$AB = AD$,$AD// BC$。
因为$AP\perp BC$,所以$AP\perp AD$,即$\angle PAD = 90^{\circ}$。
又因为$\angle PAQ=\angle B$,$AD// BC$,所以$\angle B+\angle BAD = 180^{\circ}$,$\angle PAQ+\angle PAD+\angle QAD = 180^{\circ}$。
把$\angle PAQ=\angle B$,$\angle PAD = 90^{\circ}$代入$\angle PAQ+\angle PAD+\angle QAD = 180^{\circ}$和$\angle B+\angle BAD = 180^{\circ}$中,可得$\angle BAD=\angle PAQ + \angle QAD$,$\angle BAD=\angle B+\angle BAP$,所以$\angle BAP=\angle QAD$。
因为$AD// BC$,$AP\perp BC$,所以$\angle APB=\angle AQD = 90^{\circ}$。
在$\triangle ABP$和$\triangle ADQ$中,$\begin{cases}\angle BAP=\angle QAD\\\angle APB=\angle AQD\\AB = AD\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等)可得$\triangle ABP\cong\triangle ADQ$,所以$AP = AQ$。
$(2)$ 判断$(1)$中的结论是否成立并证明
解:
$(1)$中的结论仍然成立,即$AP = AQ$。
证明:过点$A$作$AE\perp BC$于点$E$,$AF\perp CD$于点$F$。
因为四边形$ABCD$是菱形,所以$AB = AD$,$\angle B=\angle D$,$BC = CD$,$AE = AF$(菱形的面积$S = BC× AE=CD× AF$)。
因为$\angle PAQ=\angle B$,$\angle AEB=\angle AFD = 90^{\circ}$,$\angle B+\angle BAE+\angle AEB = 180^{\circ}$,$\angle PAQ+\angle PAE+\angle FAQ = 180^{\circ}$,所以$\angle BAE=\angle FAQ$。
又因为$\angle AEP=\angle AFQ = 90^{\circ}$,$AE = AF$。
在$\triangle AEP$和$\triangle AFQ$中,$\begin{cases}\angle AEP=\angle AFQ\\AE = AF\\\angle PAE=\angle QAF\end{cases}$,根据$ASA$(两角及其夹边对应相等的两个三角形全等)可得$\triangle AEP\cong\triangle AFQ$,所以$AP = AQ$。
$(3)$ 求四边形$APCQ$的面积
因为$AB = 4$,$\angle B = 60^{\circ}$,过$A$作$AE\perp BC$于$E$。
在$Rt\triangle ABE$中,$\sin B=\frac{AE}{AB}$,则$AE = AB\sin60^{\circ}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$。
$S_{\triangle ABC}=\frac{1}{2}BC× AE$,因为$BC = AB = 4$,所以$S_{\triangle ABC}=\frac{1}{2}×4×2\sqrt{3}=4\sqrt{3}$。
由$(2)$可知$\triangle AEP\cong\triangle AFQ$,所以$S_{四边形APCQ}=S_{\triangle AEC}+S_{\triangle ACQ}=S_{\triangle AEC}+S_{\triangle AEP}=S_{\triangle ABC}=4\sqrt{3}$。
综上,答案依次为:$(1)$ 证明见上述过程;$(2)$ 成立,证明见上述过程;$(3)$$4\sqrt{3}$。
解:
因为四边形$ABCD$是菱形,所以$AB = AD$,$AD// BC$。
因为$AP\perp BC$,所以$AP\perp AD$,即$\angle PAD = 90^{\circ}$。
又因为$\angle PAQ=\angle B$,$AD// BC$,所以$\angle B+\angle BAD = 180^{\circ}$,$\angle PAQ+\angle PAD+\angle QAD = 180^{\circ}$。
把$\angle PAQ=\angle B$,$\angle PAD = 90^{\circ}$代入$\angle PAQ+\angle PAD+\angle QAD = 180^{\circ}$和$\angle B+\angle BAD = 180^{\circ}$中,可得$\angle BAD=\angle PAQ + \angle QAD$,$\angle BAD=\angle B+\angle BAP$,所以$\angle BAP=\angle QAD$。
因为$AD// BC$,$AP\perp BC$,所以$\angle APB=\angle AQD = 90^{\circ}$。
在$\triangle ABP$和$\triangle ADQ$中,$\begin{cases}\angle BAP=\angle QAD\\\angle APB=\angle AQD\\AB = AD\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等)可得$\triangle ABP\cong\triangle ADQ$,所以$AP = AQ$。
$(2)$ 判断$(1)$中的结论是否成立并证明
解:
$(1)$中的结论仍然成立,即$AP = AQ$。
证明:过点$A$作$AE\perp BC$于点$E$,$AF\perp CD$于点$F$。
因为四边形$ABCD$是菱形,所以$AB = AD$,$\angle B=\angle D$,$BC = CD$,$AE = AF$(菱形的面积$S = BC× AE=CD× AF$)。
因为$\angle PAQ=\angle B$,$\angle AEB=\angle AFD = 90^{\circ}$,$\angle B+\angle BAE+\angle AEB = 180^{\circ}$,$\angle PAQ+\angle PAE+\angle FAQ = 180^{\circ}$,所以$\angle BAE=\angle FAQ$。
又因为$\angle AEP=\angle AFQ = 90^{\circ}$,$AE = AF$。
在$\triangle AEP$和$\triangle AFQ$中,$\begin{cases}\angle AEP=\angle AFQ\\AE = AF\\\angle PAE=\angle QAF\end{cases}$,根据$ASA$(两角及其夹边对应相等的两个三角形全等)可得$\triangle AEP\cong\triangle AFQ$,所以$AP = AQ$。
$(3)$ 求四边形$APCQ$的面积
因为$AB = 4$,$\angle B = 60^{\circ}$,过$A$作$AE\perp BC$于$E$。
在$Rt\triangle ABE$中,$\sin B=\frac{AE}{AB}$,则$AE = AB\sin60^{\circ}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$。
$S_{\triangle ABC}=\frac{1}{2}BC× AE$,因为$BC = AB = 4$,所以$S_{\triangle ABC}=\frac{1}{2}×4×2\sqrt{3}=4\sqrt{3}$。
由$(2)$可知$\triangle AEP\cong\triangle AFQ$,所以$S_{四边形APCQ}=S_{\triangle AEC}+S_{\triangle ACQ}=S_{\triangle AEC}+S_{\triangle AEP}=S_{\triangle ABC}=4\sqrt{3}$。
综上,答案依次为:$(1)$ 证明见上述过程;$(2)$ 成立,证明见上述过程;$(3)$$4\sqrt{3}$。
查看更多完整答案,请扫码查看


