《2025年本土假期作业巩固训练八年级数学北师大版》

14. 如图,已知线段 $ A B $,点 $ C $ 是线段 $ A B $ 的中点,点 $ D $ 在直线 $ A B $ 上,线段 $ C D $ 绕点 $ C $ 顺时针旋转 $ 90 ^ { \circ } $ 得到线段 $ C E $,过点 $ B $ 作 $ B F \perp A E $ 交 $ A E $ 的延长线于点 $ F $,交直线 $ D E $ 于点 $ G $.
(1)补全图形；
(2)求 $ A E $ 与 $ B G $ 的数量关系；
(3)在补全的图形中,用等式表示 $ A B $,$ E G $,$ C D $ 的数量关系,并予以证明.

答案：

(1)解：补全图形如图1.
(2)解：$AE=BG$，理由如下：连接$BE$，如图2，由题意，得$CD=CE$，$AB⊥CE$，$\therefore ∠CDE=∠CED=45^{\circ}$，$\because$点$C$是线段$AB$的中点，$\therefore CE$垂直平分线段$AB$，$\therefore AE=BE$，$\therefore ∠A=∠ABE$，$\because ∠CDE=∠CED=45^{\circ}$，$\therefore ∠A+∠AED=45^{\circ}$，$\because ∠AED=∠GEF$，$\therefore ∠A+∠GEF=45^{\circ}$，$\because BF⊥AE$，$\therefore ∠G+∠GEF=90^{\circ}$，$\therefore ∠G=90^{\circ}-∠GEF$，$\because ∠A=∠ABE$，$∠A+∠ABE=∠FEB$，$\therefore 2∠A=∠FEB$，$\therefore ∠BEG=∠FEB+∠GEF=2∠A+∠GEF$，$\because ∠A+∠GEF=45^{\circ}$，$\therefore ∠BEG=90^{\circ}-∠GEF$，$\therefore ∠BEG=∠G$，$\therefore BE=BG$，$\therefore AE=BG$.
(3)$\sqrt{2}EG+2CD=AB$.

15. 有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知 $ \angle B = \angle D = 90 ^ { \circ } $,$ A D = C D $,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗？画出图形,并说明理由.

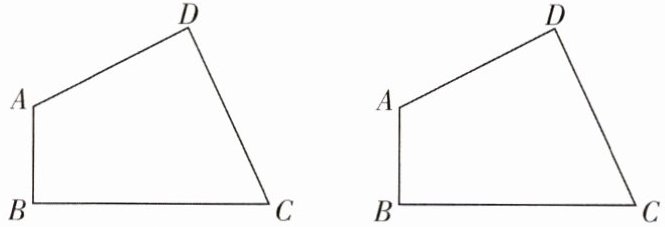
答案：
解：①将一块四边形木板拼成正方形如图1，过点$D$作$DE⊥BC$于点$E$，沿$DE$所在直线切割木板，将$\triangle DEC$绕点$D$顺时针旋转$90^{\circ}$，即可得到正方形$BEDF$，由旋转的性质，可知$\triangle AFD≌\triangle CED$，$\therefore FD=DE$，又$\because ∠B=∠F=∠BED=90^{\circ}$，$\therefore$四边形$FBED$为正方形;②将两块四边形木板拼成正方形如图2，将一块四边形木板沿$BD$所在直线切割，将$\triangle DBC$绕点$D$顺时针旋转$90^{\circ}$，即可得出等腰直角$\triangle B'BD$，另一块木板同理，可得出正方形$B'EBD$.