第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
13. 若 a 的 3 倍与 2 的差是负数,则可列出不等式
3a - 2<0
.
答案:
3a - 2<0
14. 若关于 x 的不等式$(1-a)x>2可化为x<\frac{2}{1-a}$,则 a 的取值范围是
a>1
.
答案:
a>1
15. 已知关于 x 的方程$\frac{5x-2m}{4}= \frac{m}{2}-\frac{5}{4}$的解为非负数,则 m 的取值范围是
m≥$\frac{5}{4}$
.
答案:
m≥$\frac{5}{4}$
16. 《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某兴趣小组阅读四大名著的人数同时满足以下三个条件:(1)阅读过《西游记》的人数多于阅读过《水浒传》的人数;(2)阅读过《水浒传》的人数多于阅读过《三国演义》的人数;(3)阅读过《三国演义》的人数的 2 倍多于阅读过《西游记》的人数.若阅读过《三国演义》的人数为 4,则阅读过《水浒传》的人数的最大值为
6
.
答案:
6
17. 对于任意一个有理数 m,我们规定$[m]$表示不大于 m 的最大整数.例如$[1.2]= 1,[3]= 3,[-2.5]= -3$.若$[\frac{x+2}{3}]= -5$,则整数 x 的值是
−17或−16或−15
.
答案:
−17或−16或−15
18. 定义一种法则“⊕”如下:$a⊕b= \left\{\begin{array}{l}a(a>b),\\ b(a≤b).\end{array} \right.$例如:$1⊕2= 2$.若$(-3p+5)⊕11= 11$,则 p 的取值范围是____
p≥−2
.
答案:
p≥−2
19. 解不等式$\frac{1+2x}{3}+1≥\frac{1+x}{2}$,并把它的解集在数轴上表示出来.
答案:
解:
两边同乘6:
去括号:
移项:
合并同类项:
数轴表示:(画一条数轴,在-5处用实心圆点表示,并向右画线)

解:
两边同乘6:
去括号:
移项:
合并同类项:
数轴表示:(画一条数轴,在-5处用实心圆点表示,并向右画线)

20. 解不等式组:$\left\{\begin{array}{l}3x-5<x+1,\\ \frac{3x-4}{6}≤\frac{2x-1}{3},\end{array} \right.$并把它的解集在数轴上表示出来.
答案:
解:解不等式$3x - 5 < x + 1$,
$3x - x < 1 + 5$,
$2x < 6$,
$x < 3$。
解不等式$\frac{3x - 4}{6} \leq \frac{2x - 1}{3}$,
两边同乘6得:$3x - 4 \leq 2(2x - 1)$,
$3x - 4 \leq 4x - 2$,
$3x - 4x \leq -2 + 4$,
$-x \leq 2$,
$x \geq -2$。
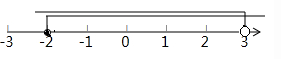
不等式组的解集为$-2 \leq x < 3$。
(数轴表示:画一条数轴,标出原点、正方向和单位长度,在数轴上找到表示$-2$的点,用实心圆点表示,找到表示$3$的点,用空心圆圈表示,然后连接两点之间的部分。)
解:解不等式$3x - 5 < x + 1$,
$3x - x < 1 + 5$,
$2x < 6$,
$x < 3$。
解不等式$\frac{3x - 4}{6} \leq \frac{2x - 1}{3}$,
两边同乘6得:$3x - 4 \leq 2(2x - 1)$,
$3x - 4 \leq 4x - 2$,
$3x - 4x \leq -2 + 4$,
$-x \leq 2$,
$x \geq -2$。
不等式组的解集为$-2 \leq x < 3$。
(数轴表示:画一条数轴,标出原点、正方向和单位长度,在数轴上找到表示$-2$的点,用实心圆点表示,找到表示$3$的点,用空心圆圈表示,然后连接两点之间的部分。)

21. 某商店准备销售甲、乙两种商品共 80 件,已知 2 件甲种商品与 3 件乙种商品的销售利润相同,3 件甲种商品比 2 件乙商品的销售利润多 150 元.
(1)每件甲种商品与每件乙种商品的销售利润各是多少元?
(2)若甲、乙两种商品的销售总利润不低于 6600 元,则至少销售甲种商品多少件?
(1)每件甲种商品与每件乙种商品的销售利润各是多少元?
(2)若甲、乙两种商品的销售总利润不低于 6600 元,则至少销售甲种商品多少件?
答案:
(1)解:设甲种商品的销售利润为x元,则乙种商品的销售利润为$\frac{2}{3}$x元,依题意,得
3x - 2×$\frac{2}{3}$x = 150,解得x = 90,
$\frac{2}{3}$x = $\frac{2}{3}$×90 = 60.
故每件甲种商品与每件乙种商品的销售利润各是90元,60元.
(2)解:设销售甲种商品a件,依题意,得
90a + 60(80 - a)≥6600,解得a≥60.
故至少销售甲种商品60件.
(1)解:设甲种商品的销售利润为x元,则乙种商品的销售利润为$\frac{2}{3}$x元,依题意,得
3x - 2×$\frac{2}{3}$x = 150,解得x = 90,
$\frac{2}{3}$x = $\frac{2}{3}$×90 = 60.
故每件甲种商品与每件乙种商品的销售利润各是90元,60元.
(2)解:设销售甲种商品a件,依题意,得
90a + 60(80 - a)≥6600,解得a≥60.
故至少销售甲种商品60件.
查看更多完整答案,请扫码查看


