第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例 1 如下图是一次函数$y= -\frac{3}{2}x+3$的图象,当$-3<y<3$时,x 的取值范围是(

A.$x>4$
B.$0<x<2$
C.$0<x<4$
D.$2<x<4$
C
)
A.$x>4$
B.$0<x<2$
C.$0<x<4$
D.$2<x<4$
答案:
C
例 2 直线$l_1:y= k_1x+b与直线l_2:y= k_2x$在同一平面直角坐标系中的图象如下图所示,则关于 x 的不等式$k_2x<k_1x+b$的解集为(
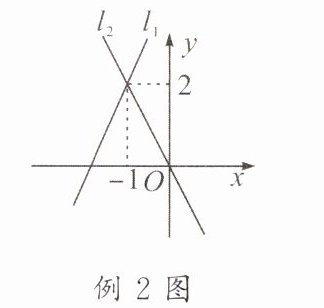
A.$x<-1$
B.$x>-1$
C.$x>2$
D.$x<2$
B
)
A.$x<-1$
B.$x>-1$
C.$x>2$
D.$x<2$
答案:
B
1. 已知函数$y_1= 2x-1,y_2= -x+3$,若$x<\frac{4}{3}$,则$y_1$
<
$y_2$.(选填“>”“=”或“<”)
答案:
解:$y_1 - y_2 = (2x - 1) - (-x + 3) = 3x - 4$
当$x < \frac{4}{3}$时,$3x - 4 < 0$,即$y_1 - y_2 < 0$
$\therefore y_1 < y_2$
<
当$x < \frac{4}{3}$时,$3x - 4 < 0$,即$y_1 - y_2 < 0$
$\therefore y_1 < y_2$
<
2. 已知一次函数$y_1= kx-2k$(k 是常数)和$y_2= -x+1$.
(1)无论 k 取何值,$y_1= kx-2k$(k 是常数)的图象都经过同一个点,则这个点的坐标是
(2)若无论 x 取何值,$y_1>y_2$,则 k 的值是
(1)无论 k 取何值,$y_1= kx-2k$(k 是常数)的图象都经过同一个点,则这个点的坐标是
(2,0)
;(2)若无论 x 取何值,$y_1>y_2$,则 k 的值是
-1
.
答案:
(1)解:$y_1=kx-2k=k(x-2)$,当$x-2=0$,即$x=2$时,$y_1=0$,所以无论$k$取何值,函数图象都经过点$(2,0)$。
(2)解:由$y_1>y_2$得$kx-2k>-x+1$,整理得$(k+1)x>2k+1$。因为无论$x$取何值该不等式都成立,所以$\begin{cases}k+1=0\\2k+1<0\end{cases}$,解得$k=-1$。
(1)$(2,0)$;
(2)$-1$
(1)解:$y_1=kx-2k=k(x-2)$,当$x-2=0$,即$x=2$时,$y_1=0$,所以无论$k$取何值,函数图象都经过点$(2,0)$。
(2)解:由$y_1>y_2$得$kx-2k>-x+1$,整理得$(k+1)x>2k+1$。因为无论$x$取何值该不等式都成立,所以$\begin{cases}k+1=0\\2k+1<0\end{cases}$,解得$k=-1$。
(1)$(2,0)$;
(2)$-1$
例 1 “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 A,B 两种型号的垃圾处理设备共 10 台.已知每台 A 型设备日处理能力为 12 t;每台 B 型设备日处理能力为 15 t;购回的设备日处理能力不低于 140 t.
(1)请你为该景区设计购买 A,B 两种设备的方案;(两种设备均要购买)
(2)已知每台 A 型设备价格为 3 万元,每台 B 型设备价格为 4.4 万元.厂家为了促销产品,规定货款不低于 40 万元时,则按 9 折优惠.问:采用(1)设计的哪种方案,可使购买费用最少? 为什么?
【思路点拨】(1)设购买 A 种设备 x 台,则购买 B 种设备$(10-x)$台,根据购回的设备日处理能力不低于 140 t 列出不等式$12x+15(10-x)≥140$,求出解集,再根据 x 为正整数,得出 x 的值为 1 或 2 或 3,进而求解即可;(2)分别求出各方案的实际购买费用,比较即可求解.
(1)请你为该景区设计购买 A,B 两种设备的方案;(两种设备均要购买)
(2)已知每台 A 型设备价格为 3 万元,每台 B 型设备价格为 4.4 万元.厂家为了促销产品,规定货款不低于 40 万元时,则按 9 折优惠.问:采用(1)设计的哪种方案,可使购买费用最少? 为什么?
【思路点拨】(1)设购买 A 种设备 x 台,则购买 B 种设备$(10-x)$台,根据购回的设备日处理能力不低于 140 t 列出不等式$12x+15(10-x)≥140$,求出解集,再根据 x 为正整数,得出 x 的值为 1 或 2 或 3,进而求解即可;(2)分别求出各方案的实际购买费用,比较即可求解.
答案:
(1)解:设购买A种设备x台,则购买B种设备(10 - x)台,
根据题意,得12x + 15(10 - x)≥140,
解得x≤3$\frac{1}{3}$,
∵x为正整数,
∴x = 1,2,3,
∴该景区有三种设计方案:
方案一:购买A种设备1台,B种设备9台;
方案二:购买A种设备2台,B种设备8台;
方案三:购买A种设备3台,B种设备7台.
(2)解:各方案购买费用分别为:
方案一:3×1 + 4.4×9 = 42.6>40,
实际付款:42.6×0.9 = 38.34(万元);
方案二:3×2 + 4.4×8 = 41.2>40,
实际付款:41.2×0.9 = 37.08(万元);
方案三:3×3 + 4.4×7 = 39.8<40,
实际付款:39.8万元;
∵37.08<38.34<39.8,
∴采用设计的第二种方案,购买费用最少.
(1)解:设购买A种设备x台,则购买B种设备(10 - x)台,
根据题意,得12x + 15(10 - x)≥140,
解得x≤3$\frac{1}{3}$,
∵x为正整数,
∴x = 1,2,3,
∴该景区有三种设计方案:
方案一:购买A种设备1台,B种设备9台;
方案二:购买A种设备2台,B种设备8台;
方案三:购买A种设备3台,B种设备7台.
(2)解:各方案购买费用分别为:
方案一:3×1 + 4.4×9 = 42.6>40,
实际付款:42.6×0.9 = 38.34(万元);
方案二:3×2 + 4.4×8 = 41.2>40,
实际付款:41.2×0.9 = 37.08(万元);
方案三:3×3 + 4.4×7 = 39.8<40,
实际付款:39.8万元;
∵37.08<38.34<39.8,
∴采用设计的第二种方案,购买费用最少.
查看更多完整答案,请扫码查看


