《2025年高中必修课程复习与检测数学》

10. 已知某班一个学习小组的数学考试成绩如下：92，90，85，93，95，86，88，91，则它的样本方差为 （ ）
A. 5.5
B. 6.5
C. 10.5
D. 9.5

答案： C 解析：直接利用公式计算.

11. 样本中共有5个个体，其值分别为$a$，0，1，2，3. 若该样本的平均值为1，则样本方差为 （ ）
A. $\sqrt{\frac{6}{5}}$
B. $\frac{6}{5}$
C. $\sqrt{2}$
D. 2

答案： D 解析：由题意知$\frac{1}{5}(a + 0 + 1 + 2 + 3)=1$，解得$a = - 1$.
$\therefore$样本方差为$s^{2}=\frac{1}{5}[(-1 - 1)^{2}+(0 - 1)^{2}+(1 - 1)^{2}+(2 - 1)^{2}+(3 - 1)^{2}]=2$.

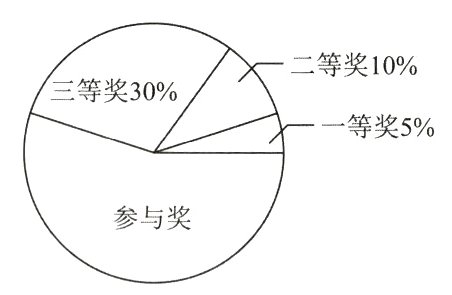
12. 某班级在一次数学竞赛中为全班学生设置了一等奖、二等奖、三等奖以及参与奖，各类奖品的单价分别为：一等奖18元、二等奖8元、三等奖4元、参与奖2元，获奖人数的分配情况如图，则以下说法不正确的是 （ ）
A. 获得参与奖的人数最多
B. 各个奖项中参与奖的总费用最高
C. 购买每件奖品费用的平均数为4元
D. 购买的三等奖的奖品数是一、二等奖的奖品数和的二倍
　　　　　　　　　　　　　　　　　　　

答案： B 解析：由题意，设全班人数为$a$，由扇形图可知，一等奖占5%，二等奖占10%，三等奖占30%，则参与奖占55%. 获得参与奖的人数最多，故A正确；各奖项的费用为一等奖$5\%a\times18 = 0.9a$，二等奖$10\%a\times8 = 0.8a$，三等奖$30\%a\times4 = 1.2a$，参与奖$55\%a\times2 = 1.1a$，可知各个奖项中三等奖的总费用最高，故B错误；每件奖品的平均费用为$5\%\times18 + 10\%\times8 + 30\%\times4 + 55\%\times2 = 4$（元），故C正确；一等奖奖品数为$5\%a$，二等奖奖品数为$10\%a$，三等奖奖品数为$30\%a$，故D正确.

13. 已知数据：①18，32， - 6，14，8，12；②21，4，7，14， - 3，11；③5，4，6，5，4，3，1，4；④ - 1，3，1，0，0， - 3. 其中平均数与中位数相等的数据 （ ）
A. ①
B. ②
C. ③
D. ①②③④

答案： D 解析：运用计算公式：$\overline{x}=\frac{1}{n}(x_{1}+x_{2}+\cdots +x_{n})$，可知四组数据的平均数分别为13，9，4，0. 根据中位数的定义：把每组数据从小到大排列，取中间一位数（或中间两位数的平均数）为该组数据的中位数，可知四组数据的中位数分别为13，9，4，0. 故每组数据的平均数和中位数均对应相等.

14. 如果一组数据按从大到小排列，得到15，10，$x$，5， - 1的平均数为7，则这组数据的$x$的值和方差分别为 （ ）
A. 4，$\frac{86}{5}$
B. 6，$\frac{86}{5}$
C. 6，$\frac{142}{5}$
D. 4，$\frac{114}{5}$

答案： C

15. 若数据$x_1$，$x_2$，…，$x_n$的平均数为$\overline{x}$，方差为$s^2$，则$2x_1 + 3$，$2x_2 + 3$，…，$2x_n + 3$的平均数和方差分别为 （ ）
A. $\overline{x}$和$s^2$
B. $2\overline{x}+3$和$4s^2$
C. $2\overline{x}+3$和$s^2$
D. $2\overline{x}+3$和$4s^2 + 12s + 9$

答案： B 解析：平均数为$\frac{1}{n}(2x_{1}+3 + 2x_{2}+3+\cdots + 2x_{n}+3)=\frac{1}{n}[2(x_{1}+x_{2}+\cdots +x_{n})+3n]=2\overline{x}+3$；方差为$\frac{1}{n}\{[(2x_{1}+3)-(2\overline{x}+3)]^{2}+[(2x_{2}+3)-(2\overline{x}+3)]^{2}+\cdots +[(2x_{n}+3)-(2\overline{x}+3)]^{2}\}=\frac{1}{n}[4(x_{1}-\overline{x})^{2}+4(x_{2}-\overline{x})^{2}+\cdots +4(x_{n}-\overline{x})^{2}]=4s^{2}$.