《2025年高中必修课程复习与检测数学》

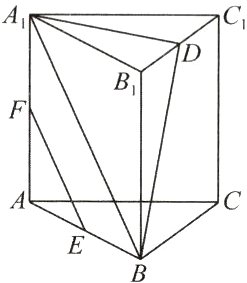
24. 如图，在直三棱柱ABC - A₁B₁C₁中，D，E，F分别是B₁C₁，AB，AA₁的中点.
(1)求证：EF//平面A₁BD；
(2)若A₁B₁ = A₁C₁，求证：平面A₁BD⊥平面BB₁C₁C.
　　　　　　　　　　　　　　　　　　　　　　　　

答案： 证明：
(1)$\because$在直三棱柱$ABC - A_{1}B_{1}C_{1}$中，$E$，$F$分别是$AB$，$AA_{1}$的中点，$\therefore EF// A_{1}B$。
$\because EF\not\subset$平面$A_{1}BD$，$A_{1}B\subset$平面$A_{1}BD$，$\therefore EF//$平面$A_{1}BD$。
(2)$\because A_{1}B_{1}=A_{1}C_{1}$，$D$是$B_{1}C_{1}$的中点，$\therefore A_{1}D\perp B_{1}C_{1}$。
$\because$在直三棱柱$ABC - A_{1}B_{1}C_{1}$中，$BB_{1}\perp$平面$A_{1}B_{1}C_{1}$，且$A_{1}D\subset$平面$A_{1}B_{1}C_{1}$，$\therefore A_{1}D\perp BB_{1}$。
$\because B_{1}C_{1}\cap BB_{1}=B_{1}$，$B_{1}C_{1}$，$BB_{1}\subset$平面$BB_{1}C_{1}C$，$\therefore A_{1}D\perp$平面$BB_{1}C_{1}C$。
$\because A_{1}D\subset$平面$A_{1}BD$，$\therefore$平面$A_{1}BD\perp$平面$BB_{1}C_{1}C$。