《2025年高中必修课程复习与检测数学》

16. 下列关于棱柱的说法：
①所有的面都是平行四边形；
②每一个面都不会是三角形；
③两底面平行，并且各侧棱也平行；
④被平面截成的两部分可以都是棱柱.
其中说法正确的有________(填序号).

答案： ③④ 解析：①错误，棱柱的底面不一定是平行四边形；②错误，棱柱的底面可以是三角形；③正确，由棱柱的定义易知；④正确，棱柱可以被平行于底面的平面截成两个棱柱。所以说法正确的序号有③④。

17. 有一个棱长为3的正方体礼物需要用一个球形包装，则球的最小直径为_______.

答案： $3\sqrt{3}$

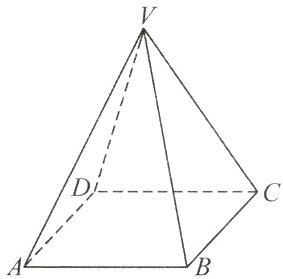
18. 如图，在四棱锥V - ABCD中，底面ABCD是边长为2的正方形，其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形，则二面角V - AB - C的度数是_______.
　　　　　　　　　　　　

答案：
$60^{\circ}$ 解析：如图，取$AB$的中点$E$，$CD$的中点$F$，连接$VE$，$EF$，$VF$，由题意知，$AB\perp VE$，$AB\perp EF$，所以$\angle VEF$为二面角$V - AB - C$的平面角。易知$\triangle VEF$为正三角形，所以$\angle VEF = 60^{\circ}$。

19. 给出下列命题：
(1)若平面α内有两条直线分别平行于平面β，则α//β；
(2)若平面α内任意一条直线与平面β平行，则α//β；
(3)过已知平面外一条直线，必能作出一个平面与已知平面平行；
(4)不重合的平面α，β，γ，若α//γ，β//γ，则有α//β.
其中正确的命题是_______(填写序号).

答案：
(2)
(4) 解析：
(1)错误，平面$\alpha$内有两条相交直线分别平行于平面$\beta$，则$\alpha//\beta$；
(2)由平面与平面平行的定义知正确；
(3)错误，若已知直线与平面相交，则无法过此直线作已知平面的平行平面；
(4)由面面平行的传递性可知正确。