《2025年高中必修课程复习与检测数学》

16. $(\boldsymbol{a}+9\boldsymbol{b}-2\boldsymbol{c})+(\boldsymbol{b}+2\boldsymbol{c})=$________.

答案： $\boldsymbol{a}+10\boldsymbol{b}$

17. 已知向量$\boldsymbol{a}$，$\boldsymbol{b}$的夹角为$45^{\circ}$，且$|\boldsymbol{a}| = 4$，$(\frac{1}{2}\boldsymbol{a}+\boldsymbol{b})\cdot(2\boldsymbol{a}-3\boldsymbol{b}) = 12$，则$|\boldsymbol{b}| =$________；$\boldsymbol{b}$在$\boldsymbol{a}$方向上的投影等于________.

答案： $\sqrt{21}$ 解析：$\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}|\cdot|\boldsymbol{b}|\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle=4|\boldsymbol{b}|\cos45^{\circ}=2\sqrt{2}|\boldsymbol{b}|$.
又$(\frac{1}{2}\boldsymbol{a}+\boldsymbol{b})\cdot(2\boldsymbol{a}-3\boldsymbol{b})=|\boldsymbol{a}|^{2}+\frac{1}{2}\boldsymbol{a}\cdot\boldsymbol{b}-3|\boldsymbol{b}|^{2}=16+\sqrt{2}|\boldsymbol{b}|-3|\boldsymbol{b}|^{2}=12$，
解得$|\boldsymbol{b}|=\sqrt{2}$或$|\boldsymbol{b}|=-\frac{2}{3}\sqrt{2}$(舍去).
$\boldsymbol{b}$在$\boldsymbol{a}$上的投影为$|\boldsymbol{b}|\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle=\sqrt{2}\cos45^{\circ}=1$.

18. 在△ABC中，$a = 2$，$c = \frac{2\sqrt{3}}{3}$，$A = 60^{\circ}$，则$C$的值为________.

答案： $30^{\circ}$

19. 在△ABC中，内角A，B，C所对的边分别为a，b，c. 已知△ABC的面积为$3\sqrt{15}$，$b - c = 2$，$\cos A = -\frac{1}{4}$，则$a$的值为________.

答案： 8 解析：$\because0\lt A\lt\pi$，
$\therefore\sin A=\sqrt{1-\cos^{2}A}=\frac{\sqrt{15}}{4}$.
又$S_{\triangle ABC}=\frac{1}{2}bc\sin A=\frac{\sqrt{15}}{8}bc=3\sqrt{15}$，
$\therefore bc = 24$，解方程组$\begin{cases}b - c = 2,\\bc = 24,\end{cases}$得$b = 6$，$c = 4$.
由余弦定理得$a^{2}=b^{2}+c^{2}-2bc\cos A=6^{2}+4^{2}-2\times6\times4\times(-\frac{1}{4})=64$，所以$a = 8$.

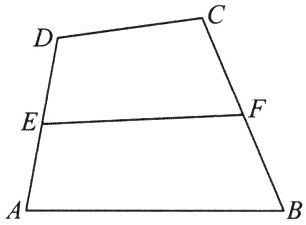
20. 如图，四边形ABCD的边AD，BC的中点分别为E，F，求证：$\overrightarrow{EF}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{DC})$.

答案：
证明：$\overrightarrow{EF}=\frac{1}{2}(\overrightarrow{EB}+\overrightarrow{EC})$
$=\frac{1}{2}(\overrightarrow{EA}+\overrightarrow{AB}+\overrightarrow{ED}+\overrightarrow{DC})$
$=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{DC})$.
$(\because\overrightarrow{EA}+\overrightarrow{ED}=\mathbf{0})$