《2025年赢在微点高中数学选择性必修第一册A版》

1. 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，下列各对向量夹角为$45^{\circ}$的是（ ）
A. $\overrightarrow{AB}$与$\overrightarrow{A_{1}C_{1}}$
B. $\overrightarrow{AB}$与$\overrightarrow{C_{1}A_{1}}$
C. $\overrightarrow{AB}$与$\overrightarrow{A_{1}D_{1}}$
D. $\overrightarrow{AB}$与$\overrightarrow{B_{1}A_{1}}$

答案： A解析 四个选项中两个向量的夹角依次是 $45^{\circ}$，$135^{\circ}$，$90^{\circ}$，$180^{\circ}$。故选 A。

2. 在棱长为$1$的正四面体$ABCD$中，$E$，$F$分别是$BC$，$AD$的中点，则$\overrightarrow{AE}\cdot\overrightarrow{AF}=$（ ）
A. $0$
B. $\frac{1}{2}$
C. $-\frac{1}{4}$
D. $\frac{1}{4}$

答案： D解析 $\overrightarrow{AE}\cdot\overrightarrow{AF}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})\cdot\frac{1}{2}\overrightarrow{AD}=\frac{1}{4}(\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{AC}\cdot\overrightarrow{AD})=\frac{1}{4}$。

3. 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$E$是上底面$A_{1}B_{1}C_{1}D_{1}$的中心，则$AC_{1}$与$CE$的位置关系是（ ）
A. 重合
B. 平行
C. 垂直
D. 无法确定

答案： C解析 设正方体的棱长为 1，$\overrightarrow{AC_{1}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_{1}}$，$\overrightarrow{CE}=\overrightarrow{CC_{1}}+\overrightarrow{C_{1}E}=\overrightarrow{AA_{1}}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})$，于是 $\overrightarrow{AC_{1}}\cdot\overrightarrow{CE}=(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_{1}})\cdot[\overrightarrow{AA_{1}}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})]=0-\frac{1}{2}-0 + 0 - 0-\frac{1}{2}+1 - 0 - 0 = 0$，故 $\overrightarrow{AC_{1}}\perp\overrightarrow{CE}$，即 $AC_{1}$ 与 $CE$ 垂直。

4. 如图，四面体$ABCD$的每条棱长都等于$2$，点$E$，$F$分别为棱$AB$，$AD$的中点，则$\vert\overrightarrow{BC}-\overrightarrow{EF}\vert=$ ，$\overrightarrow{EF}$与$\overrightarrow{AC}$所成的角为 。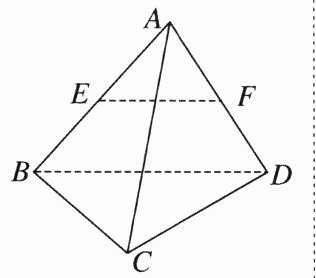

答案： 解析 $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BD}$，$\overrightarrow{BD}\cdot\overrightarrow{BC}=2\times2\times\cos\frac{\pi}{3}=2$，故 $|\overrightarrow{BC}-\overrightarrow{EF}|^{2}=|\overrightarrow{BC}-\frac{1}{2}\overrightarrow{BD}|^{2}=\overrightarrow{BC}^{2}-\overrightarrow{BC}\cdot\overrightarrow{BD}+\frac{1}{4}\overrightarrow{BD}^{2}=4 - 2+\frac{1}{4}\times4 = 3$。故 $|\overrightarrow{BC}-\overrightarrow{EF}|=\sqrt{3}$。又因为 $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{AD}-\overrightarrow{AB})$，故 $\overrightarrow{AC}\cdot\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AC}\cdot(\overrightarrow{AD}-\overrightarrow{AB})=\frac{1}{2}(\overrightarrow{AC}\cdot\overrightarrow{AD}-\overrightarrow{AC}\cdot\overrightarrow{AB}) = 0$，因为 $\langle\overrightarrow{EF},\overrightarrow{AC}\rangle\in[0,\pi]$，所以 $\langle\overrightarrow{EF},\overrightarrow{AC}\rangle=\frac{\pi}{2}$。

5. 如图，在空间四边形$OABC$中，$OA$，$OB$，$OC$两两成$60^{\circ}$角，且$OA = OB = OC = 2$，$E$为$OA$的中点，$F$为$BC$的中点，试求$E$，$F$间的距离。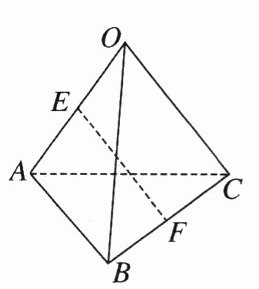

答案： 解 $\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AF}=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}[(\overrightarrow{OB}-\overrightarrow{OA})+(\overrightarrow{OC}-\overrightarrow{OA})]=-\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$，所以 $\overrightarrow{EF}^{2}=\frac{1}{4}\overrightarrow{OA}^{2}+\frac{1}{4}\overrightarrow{OB}^{2}+\frac{1}{4}\overrightarrow{OC}^{2}+2\times(-\frac{1}{2})\times\frac{1}{2}\overrightarrow{OA}\cdot\overrightarrow{OB}+2\times(-\frac{1}{2})\times\frac{1}{2}\overrightarrow{OA}\cdot\overrightarrow{OC}+2\times\frac{1}{2}\times\frac{1}{2}\overrightarrow{OB}\cdot\overrightarrow{OC}=2$。所以 $|\overrightarrow{EF}|=\sqrt{2}$，即 $E$，$F$ 间的距离为 $\sqrt{2}$。

1. 空间向量基本定理
如果三个向量$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$不共面，那么对任意一个空间向量$\boldsymbol{p}$，存在________有序实数组$(x$，$y$，$z)$，使得$\boldsymbol{p}=$________。其中$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$叫做空间的一个_______，$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$都叫做________。

答案： 唯一的@@$x\boldsymbol{a} + y\boldsymbol{b} + z\boldsymbol{c}$@@基底@@基向量

2. 空间向量的正交分解
（1）单位正交基底。
如果空间的一个基底中的三个基向量________，且长度都为 1，那么这个基底叫做________，常用$\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$表示。
（2）对空间中的任意向量$\boldsymbol{a}$，均可以分解为三个向量$x\boldsymbol{i}$，$y\boldsymbol{j}$，$z\boldsymbol{k}$，使$\boldsymbol{a}=$________。把一个空间向量分解为三个________的向量，叫做把空间向量进行正交分解。

答案： 两两垂直@@单位正交基底@@$x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k}$@@两两垂直