《2025年赢在微点高中数学选择性必修第一册A版》

1. 直线$2x + y + 8 = 0$和直线$x + y - 1 = 0$的交点坐标是（ ）
A. ( - 9, - 10)
B. ( - 9,10)
C. (9,10)
D. (9, - 10)

答案： B 解析：解方程组$\begin{cases}2x + y + 8 = 0\\x + y - 1 = 0\end{cases}$，得$\begin{cases}x = -9\\y = 10\end{cases}$，即交点坐标是$(-9,10)$。

2. 已知直角坐标平面上连接点$( - 2,5)$和点$M$的线段的中点是$(1,0)$，那么点$M$到原点的距离为（ ）
A. 41
B. $\sqrt{41}$
C. $\sqrt{39}$
D. 39

答案： B 解析：设$M(x,y)$，由题意得$\begin{cases}1=\frac{-2 + x}{2}\\0=\frac{5 + y}{2}\end{cases}$，解得$\begin{cases}x = 4\\y = -5\end{cases}$，所以$M(4,-5)$。则$M$到原点的距离为$\sqrt{(4 - 0)^2+(-5 - 0)^2}=\sqrt{41}$。

3. 已知直线$l_1:ax + y - 6 = 0$与$l_2:x + (a - 2)y + a - 1 = 0$相交于点$P$，若$l_1\perp l_2$，则点$P$的坐标为________。

答案： $(3,3)$ 解析：因为直线$l_1:ax + y - 6 = 0$与$l_2:x+(a - 2)y + a - 1 = 0$相交于点$P$，且$l_1\perp l_2$，所以$a\times1 + 1\times(a - 2)=0$，解得$a = 1$，联立方程$\begin{cases}x + y - 6 = 0\\x - y = 0\end{cases}$，解得$\begin{cases}x = 3\\y = 3\end{cases}$，所以点$P$的坐标为$(3,3)$。

4. 直线$(m - 1)x + (2m - 1)y = m - 5$必通过定点________。

答案： $(9,-4)$ 解析：将原方程按$m$的降幂排列，整理得$(x + 2y - 1)m-(x + y - 5)=0$，此式对于$m$的任意实数值都成立，根据恒等式的要求，$m$的一次项系数与常数项均等于$0$，故有$\begin{cases}x + 2y - 1 = 0\\x + y - 5 = 0\end{cases}$，解得$\begin{cases}x = 9\\y = -4\end{cases}$。所以$m$为任意实数时，所给直线必通过定点$(9,-4)$。

5. 求经过直线$l_1:3x + 2y - 1 = 0$和$l_2:5x + 2y+1 = 0$的交点，且垂直于直线$l_3:3x - 5y + 6 = 0$的直线$l$的方程。

答案： 解： 解法一：解方程组$\begin{cases}3x + 2y - 1 = 0\\5x + 2y + 1 = 0\end{cases}$，得交点坐标为$(-1,2)$。又由直线$l_3$的斜率为$\frac{3}{5}$，得直线$l$的斜率为$-\frac{5}{3}$，则直线$l$的方程为$y - 2 = -\frac{5}{3}(x + 1)$，即$5x + 3y - 1 = 0$。 解法二：由于直线$l\perp l_3$，故直线$l$满足$5x + 3y + C = 0$。又直线$l$过直线$l_1$，$l_2$的交点$(-1,2)$，故$5\times(-1)+3\times2 + C = 0$，解得$C = -1$，故直线$l$的方程为$5x + 3y - 1 = 0$。 解法三：由于直线$l$过直线$l_1$，$l_2$的交点，故直线$l$满足$3x + 2y - 1+\lambda(5x + 2y + 1)=0$，整理，得$(3 + 5\lambda)x+(2 + 2\lambda)y+(-1 + \lambda)=0$。其斜率为$-\frac{3 + 5\lambda}{2 + 2\lambda}=-\frac{5}{3}$，解得$\lambda=\frac{1}{5}$，则直线$l$的方程为$5x + 3y - 1 = 0$。

如图所示，渔民们要将船推到海里，请同学们帮助设计一下：在理论上，怎样设计能使这条路最短？

答案：

1. 点到直线的距离

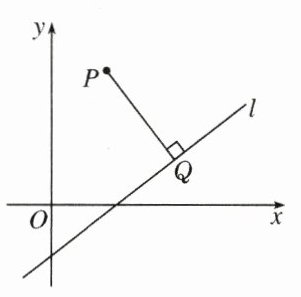
（1）概念：点$P$到直线$l$的距离，就是从点$P$到直线$l$的垂线段$PQ$的长度，如图所示，其中$Q$是________。
（2）公式：点$P(x_{0},y_{0})$到直线$l:Ax + By + C = 0(A,B$不同时为$0)$的距离d =________。
可以验证，当$A = 0$或$B = 0$时，上述公式仍然成立。

答案： 1. （1）垂足（2）$\frac{\vert Ax_0 + By_0 + C\vert}{\sqrt{A^{2}+B^{2}}}$@@

2. 两条平行直线间的距离
（1）概念：两条平行直线间的距离是指夹在这两条平行直线间的________的长。
（2）公式：两条平行直线$l_{1}:Ax + By + C_{1}=0$与$l_{2}:Ax + By + C_{2}=0(A,B$不同时为$0,C_{1}\neq C_{2})$之间的距离d =________。

答案： 2. （1）公垂线段 （2）$\frac{\vert C_1 - C_2\vert}{\sqrt{A^{2}+B^{2}}}$@@

微思考
1. 点到直线的距离公式对于$A = 0$或$B = 0$时的直线是否仍然适用？
2. 两条平行直线$2x + 3y + 2 = 0,4x + 6y + 1 = 0$间的距离是$d=\frac{\vert 2 - 1\vert}{\sqrt{2^{2}+3^{2}}}=\frac{\sqrt{13}}{13}$吗？

答案： [微思考] 1. 提示：仍然适用，但一般不用公式求解，而常用数形结合求点到直线的距离。 2. 提示：不是，应先把两直线方程中x，y的系数化为相同，再用公式求解。