2025年赢在微点高中数学选择性必修第一册A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在微点高中数学选择性必修第一册A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 空间向量的概念
(1)在空间,把具有_______和_______的量叫做空间向量,空间向量的大小叫做空间向量的_______或_______。空间向量用字母$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\cdots$表示。
空间向量也用有向线段表示,有向线段的_______表示空间向量的模。如图,向量$\boldsymbol{a}$的起点是$A$,终点是$B$,则向量$\boldsymbol{a}$也可以记作$\overrightarrow{AB}$,其模记为$|\boldsymbol{a}|$或$|\overrightarrow{AB}|$。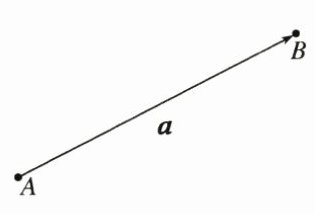
(2)几类特殊的空间向量。
|名称|定义及表示|
| ---- | ---- |
|零向量|长度为0的向量叫做零向量,记为$\boldsymbol{0}$|
|单位向量|长度为1的向量叫做单位向量|
|相反向量|与向量$\boldsymbol{a}$长度相等而方向相反的向量,叫做$\boldsymbol{a}$的相反向量,记为$-\boldsymbol{a}$|
|相等向量|方向相同且模相等的向量叫做相等向量。在空间,同向且等长的有向线段表示同一向量或相等向量|
|共线向量(平行向量)|如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量|
(1)在空间,把具有_______和_______的量叫做空间向量,空间向量的大小叫做空间向量的_______或_______。空间向量用字母$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\cdots$表示。
空间向量也用有向线段表示,有向线段的_______表示空间向量的模。如图,向量$\boldsymbol{a}$的起点是$A$,终点是$B$,则向量$\boldsymbol{a}$也可以记作$\overrightarrow{AB}$,其模记为$|\boldsymbol{a}|$或$|\overrightarrow{AB}|$。

(2)几类特殊的空间向量。
|名称|定义及表示|
| ---- | ---- |
|零向量|长度为0的向量叫做零向量,记为$\boldsymbol{0}$|
|单位向量|长度为1的向量叫做单位向量|
|相反向量|与向量$\boldsymbol{a}$长度相等而方向相反的向量,叫做$\boldsymbol{a}$的相反向量,记为$-\boldsymbol{a}$|
|相等向量|方向相同且模相等的向量叫做相等向量。在空间,同向且等长的有向线段表示同一向量或相等向量|
|共线向量(平行向量)|如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量|
答案:
大小@@方向@@长度@@模@@长度@@零向量@@模为1@@相等@@相反@@相同@@相等@@同向@@等长@@互相平行或重合@@共线向量@@
2. 空间向量的加、减、数乘运算及其运算律
|空间向量的运算| | |
| ---- | ---- | ---- |
|加法|$\boldsymbol{a}+\boldsymbol{b}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$|
|减法|$\boldsymbol{a}-\boldsymbol{b}=\overrightarrow{OA}-\overrightarrow{OC}=\overrightarrow{CA}$||
|数乘|当$\lambda>0$时,$\lambda\boldsymbol{a}=\lambda\overrightarrow{OA}=\overrightarrow{PQ}$;当$\lambda = 0$时,$\lambda\boldsymbol{a}=\boldsymbol{0}$;当$\lambda<0$时,$\lambda\boldsymbol{a}=\lambda\overrightarrow{OA}=\overrightarrow{MN}$||
|线性运算的运算律|(1)交换律:$\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{a}$;
(2)结合律:$(\boldsymbol{a}+\boldsymbol{b})+\boldsymbol{c}=\boldsymbol{a}+(\boldsymbol{b}+\boldsymbol{c})$,$\lambda(\mu\boldsymbol{a}) = (\lambda\mu)\boldsymbol{a}$;
(3)分配律:$(\lambda+\mu)\boldsymbol{a}$=_______,$\lambda(\boldsymbol{a}+\boldsymbol{b})$=_______。$(\lambda,\mu\in\mathbf{R})$| |
|空间向量的运算| | |
| ---- | ---- | ---- |
|加法|$\boldsymbol{a}+\boldsymbol{b}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$|
|减法|$\boldsymbol{a}-\boldsymbol{b}=\overrightarrow{OA}-\overrightarrow{OC}=\overrightarrow{CA}$||
|数乘|当$\lambda>0$时,$\lambda\boldsymbol{a}=\lambda\overrightarrow{OA}=\overrightarrow{PQ}$;当$\lambda = 0$时,$\lambda\boldsymbol{a}=\boldsymbol{0}$;当$\lambda<0$时,$\lambda\boldsymbol{a}=\lambda\overrightarrow{OA}=\overrightarrow{MN}$||
|线性运算的运算律|(1)交换律:$\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{a}$;
(2)结合律:$(\boldsymbol{a}+\boldsymbol{b})+\boldsymbol{c}=\boldsymbol{a}+(\boldsymbol{b}+\boldsymbol{c})$,$\lambda(\mu\boldsymbol{a}) = (\lambda\mu)\boldsymbol{a}$;
(3)分配律:$(\lambda+\mu)\boldsymbol{a}$=_______,$\lambda(\boldsymbol{a}+\boldsymbol{b})$=_______。$(\lambda,\mu\in\mathbf{R})$| |
答案:
$\lambda a+\mu a$@@$\lambda a+\lambda b$@@
3. 向量共线的充要条件
对任意两个空间向量$\boldsymbol{a},\boldsymbol{b}(\boldsymbol{b}\neq\boldsymbol{0})$,$\boldsymbol{a}//\boldsymbol{b}$的充要条件是存在_______,使$\boldsymbol{a}=\lambda\boldsymbol{b}$。
对任意两个空间向量$\boldsymbol{a},\boldsymbol{b}(\boldsymbol{b}\neq\boldsymbol{0})$,$\boldsymbol{a}//\boldsymbol{b}$的充要条件是存在_______,使$\boldsymbol{a}=\lambda\boldsymbol{b}$。
答案:
实数$\lambda$@@
5. 共面向量
(1)定义:平行于_______的向量,叫做共面向量。
(2)充要条件:如果两个向量$\boldsymbol{a},\boldsymbol{b}$不共线,那么向量$\boldsymbol{p}$与向量$\boldsymbol{a},\boldsymbol{b}$共面的充要条件是存在唯一的有序实数对$(x,y)$,使$\boldsymbol{p}$=_______。
(1)定义:平行于_______的向量,叫做共面向量。
(2)充要条件:如果两个向量$\boldsymbol{a},\boldsymbol{b}$不共线,那么向量$\boldsymbol{p}$与向量$\boldsymbol{a},\boldsymbol{b}$共面的充要条件是存在唯一的有序实数对$(x,y)$,使$\boldsymbol{p}$=_______。
答案:
同一个平面@@xa + yb@@
微思考
1. 向量共面是不是向量在同一平面内?
2. 空间任意两个向量是否一定共面?三个向量呢?
1. 向量共面是不是向量在同一平面内?
2. 空间任意两个向量是否一定共面?三个向量呢?
答案:
提示:向量共面是指向量平行于同一平面,并不一定在同一平面内,可将向量平移到同一个平面内。向量共面中的向量所在的直线可能相交、平行或异面。@@提示:空间任意两个向量总是共面的,空间任意三个向量可能共面,也可能不共面。
查看更多完整答案,请扫码查看


