《2025年赢在微点高中数学选择性必修第一册A版》

【例4】某公园有$A$，$B$两个景点，位于一条小路(直道)的同侧，分别距小路$\sqrt{2}\ km$和$2\sqrt{2}\ km$，且$A$，$B$景点间相距$2\ km$，今欲在该小路上设一观景点，使两景点在同时进入视线时有最佳观赏和拍摄效果，则观景点应设在何处？

答案： 解 所选观景点应使对两景点的视角最大。由平面几何知识知，该点应是过$A$，$B$两点的圆与小路所在的直线相切时的切点。以小路所在直线为$x$轴，点$B$在$y$轴正半轴上建立平面直角坐标系（图略）。由题意，得$A(\sqrt{2},\sqrt{2})$，$B(0,2\sqrt{2})$，设圆的方程为$(x - a)^{2}+(y - b)^{2}=b^{2}(b＞0)$，由$A$，$B$两点在圆上，得$\begin{cases}a = 0\\b = \sqrt{2}\end{cases}$或$\begin{cases}a = 4\sqrt{2}\\b = 5\sqrt{2}\end{cases}$，由实际意义知$a = 0$，$b = \sqrt{2}$，所以圆的方程为$x^{2}+(y - \sqrt{2})^{2}=2$，切点为$(0,0)$，观景点应设在$B$景点在小路的投影处。

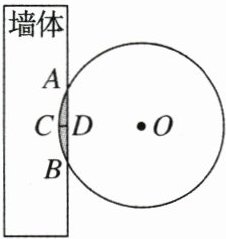
【变式训练】“圆材埋壁”是《九章算术》中的一个问题：“今有圆材，埋在壁中不知大小，以锯锯之，深一寸，锯刀长一尺，问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该木材，锯口深一寸，锯刀长一尺，问这块圆柱形木材的直径是多少？现有圆柱形木材一部分埋在墙壁中，截面如图所示，已知弦$AB = 1$尺，弓形高$CD = 1$寸，则阴影部分的面积约为（注：$\pi\approx3.14$，$\sin22.5^{\circ}\approx\frac{5}{13}$，$1$尺$ = 10$寸） （ ）

A. $6.33$平方寸
B. $6.35$平方寸
C. $6.37$平方寸
D. $6.39$平方寸

答案： A 解析 连接$OC$，$AO$（图略），$C$三点共线。设半径为$r$寸，$AD = 5$寸，则$OD=(r - 1)$寸。在$Rt\triangle OAD$中，$OA^{2}=AD^{2}+OD^{2}$，即$r^{2}=5^{2}+(r - 1)^{2}$，解得$r = 13$。所以$\sin\angle AOC=\frac{5}{13}$，所以$\angle AOC\approx22.5^{\circ}$，所以$\angle AOB\approx2\times22.5^{\circ}=45^{\circ}$。所以扇形$OAB$的面积$S_{1}=\frac{45^{\circ}\times\pi\times13^{2}}{360^{\circ}}=\frac{169\pi}{8}\approx66.33$（平方寸），$\triangle OAB$的面积$S_{2}=\frac{1}{2}\times10\times12 = 60$（平方寸），所以阴影部分的面积为$S_{1}-S_{2}=66.33 - 60 = 6.33$（平方寸）。

1. 直线$l:x - y = 1$与圆$C:x^{2}+y^{2}-4x = 0$的位置关系是 （ ）
A. 相离
B. 相切
C. 相交
D. 无法确定

答案： C 解析 圆$C$的圆心为$C(2,0)$，半径为$2$，圆心$C$到直线$l$的距离$d=\frac{\vert2 - 1\vert}{\sqrt{2}}=\frac{\sqrt{2}}{2}＜2$，所以圆$C$与直线$l$相交。

2. (多选)直线$3x + 4y = b$与圆$x^{2}+y^{2}-2x - 2y + 1 = 0$相切，则$b$的值可以为 （ ）
A. $-2$
B. $2$
C. $-12$
D. $12$

答案： BD 解析 因为直线$3x + 4y = b$与圆心为$(1,1)$，半径为$1$的圆相切，所以$\frac{\vert3 + 4 - b\vert}{\sqrt{3^{2}+4^{2}}}=1$，解得$b = 2$或$b = 12$。

3. 点$A(3,5)$是圆$x^{2}+y^{2}-4x - 8y - 80 = 0$的一条弦的中点，则这条弦所在直线的方程为 。

答案： $x + y - 8 = 0$ 解析 圆为$(x - 2)^{2}+(y - 4)^{2}=10^{2}$，圆心为$B(2,4)$，半径为$r = 10$。设这条弦所在直线为$l$，则$AB\perp l$，因为$k_{AB}=\frac{5 - 4}{3 - 2}=1$，所以直线$l$的斜率$k = - 1$。所以所求直线为$y - 5=-(x - 3)$，即$x + y - 8 = 0$。

4. 已知直线$4x - y = b$被圆$x^{2}+y^{2}-2x - 2y + 1 = 0$截得的弦长为$2$，则$b$的值为 。

答案： 3 解析 该圆的标准方程为$(x - 1)^{2}+(y - 1)^{2}=1$，故该圆的圆心$(1,1)$，半径为$1$，又直线被圆截得的弦长为$2$，所以直线必过圆心。所以$4 - 1 = b$，$b = 3$。

5. 已知台风中心从$A$地以每小时$20$千米的速度向东北方向移动，离台风中心$30$千米内的地区为危险区，城市$B$在$A$的正东$40$千米处，求$B$城市处于危险区内的时间。

答案：
解 如图，以$A$为原点，以$AB$所在直线为$x$轴建立平面直角坐标系。射线$AC$为$\angle xAy$的平分线，则台风中心在射线$AC$上移动，点$B$到$AC$的距离为$20\sqrt{2}$千米。则射线$AC$被以$B$为圆心，以$30$千米为半径的圆截得的弦长为$2\sqrt{30^{2}-(20\sqrt{2})^{2}}=20$（千米）。所以$B$城市处于危险区内的时间为$t=\frac{20}{20}=1$（小时）。