第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
知识清单
1. 等腰三角形的性质
(1) 等腰三角形的两个
(2) 等腰三角形顶角的平分线、
2. 等腰三角形的判定: 有
3. 等边三角形的性质: 等边三角形的三个内角都相等, 并且每个角都等于
4. 等边三角形的判定
(1) 三个角都相等的三角形是等边三角形.
(2) 有一个角等于 60° 的
1. 等腰三角形的性质
(1) 等腰三角形的两个
底角
相等.(2) 等腰三角形顶角的平分线、
底边上的中线及底边上的高线
互相重合.2. 等腰三角形的判定: 有
两个角
相等的三角形是等腰三角形.3. 等边三角形的性质: 等边三角形的三个内角都相等, 并且每个角都等于
60°
.4. 等边三角形的判定
(1) 三个角都相等的三角形是等边三角形.
(2) 有一个角等于 60° 的
等腰
三角形是等边三角形.
答案:
1.
(1) 底角
(2) 底边上的中线及底边上的高线
2. 两个角 3. $60^{\circ}$ 4.
(2) 等腰
(1) 底角
(2) 底边上的中线及底边上的高线
2. 两个角 3. $60^{\circ}$ 4.
(2) 等腰
例1 如下图, 在 $ \triangle ABC $ 中, $ AB = AC $, $ \angle A = 36^{\circ} $, $ BD $, $ CE $ 分别是 $ \angle ABC $, $ \angle BCD $ 的平分线, 则图中的等腰三角形有 (

A.3个
B.4个
C.5个
D.2个
C
)
A.3个
B.4个
C.5个
D.2个
答案:
C
例2 如下图, 在一个池塘两旁有一条笔直的小路 ( $ B $, $ C $ 为小路端点) 和一棵小树 ( $ A $ 为小树位置). 现测得 $ \angle ABC = 60^{\circ} $, $ \angle ACB = 60^{\circ} $, $ BC = 48 \, \text{m} $, 则 $ AC = $____

48
____ $ \text{m} $.
答案:
解:在△ABC中,
∵∠ABC=60°,∠ACB=60°,
∴∠BAC=180°-∠ABC-∠ACB=180°-60°-60°=60°,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴AC=BC,
∵BC=48m,
∴AC=48m。
答案为:48
∵∠ABC=60°,∠ACB=60°,
∴∠BAC=180°-∠ABC-∠ACB=180°-60°-60°=60°,
∴∠ABC=∠ACB=∠BAC,
∴△ABC是等边三角形,
∴AC=BC,
∵BC=48m,
∴AC=48m。
答案为:48
例3 如下图, $ AB = AC = AD $, $ \angle BAD = 80^{\circ} $, 则 $ \angle BCD $ 的度数为____
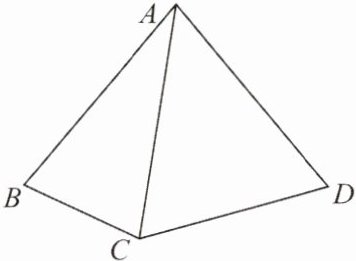
【思路点拨】在 $ \triangle ABC $ 中, $ \angle BCA = \frac{1}{2} × (180^{\circ} - \angle BAC) $, 在 $ \triangle ACD $ 中, 可得 $ \angle DCA = \frac{1}{2} (180^{\circ} - \angle CAD) $, 两式相加可求得 $ \angle BCD $ 的度数.
140°
.
【思路点拨】在 $ \triangle ABC $ 中, $ \angle BCA = \frac{1}{2} × (180^{\circ} - \angle BAC) $, 在 $ \triangle ACD $ 中, 可得 $ \angle DCA = \frac{1}{2} (180^{\circ} - \angle CAD) $, 两式相加可求得 $ \angle BCD $ 的度数.
答案:
解:设∠BAC = x,则∠CAD = ∠BAD - ∠BAC = 80° - x。
∵AB = AC,
∴∠BCA = (180° - ∠BAC)/2 = (180° - x)/2。
∵AC = AD,
∴∠DCA = (180° - ∠CAD)/2 = (180° - (80° - x))/2 = (100° + x)/2。
∠BCD = ∠BCA + ∠DCA = (180° - x)/2 + (100° + x)/2 = (180° - x + 100° + x)/2 = 280°/2 = 140°。
答案为140°
∵AB = AC,
∴∠BCA = (180° - ∠BAC)/2 = (180° - x)/2。
∵AC = AD,
∴∠DCA = (180° - ∠CAD)/2 = (180° - (80° - x))/2 = (100° + x)/2。
∠BCD = ∠BCA + ∠DCA = (180° - x)/2 + (100° + x)/2 = (180° - x + 100° + x)/2 = 280°/2 = 140°。
答案为140°
查看更多完整答案,请扫码查看


