第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. (湘西中考)若要使二次根式$\sqrt {3x-6}$有意义,则x的取值范围是 (
A.$x>2$
B.$x<2$
C.$x≤2$
D.$x≥2$
D
)A.$x>2$
B.$x<2$
C.$x≤2$
D.$x≥2$
答案:
要使二次根式$\sqrt{3x - 6}$有意义,则被开方数必须是非负数,即:
$3x - 6 \geq 0$
解不等式:
$3x \geq 6$
$x \geq 2$
答案:D
$3x - 6 \geq 0$
解不等式:
$3x \geq 6$
$x \geq 2$
答案:D
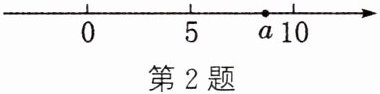
2. 若实数a在数轴上的对应点的位置如图所示,则化简$\sqrt {(a-4)^{2}}-\sqrt {(a-11)^{2}}$的结果是 (
A.7
B.-7
C.$2a-15$
D.$15-2a$
C
)
A.7
B.-7
C.$2a-15$
D.$15-2a$
答案:
由数轴可知,$5 < a < 10$。
因为$a < 10 < 11$,所以$a - 4 > 0$,$a - 11 < 0$。
$\sqrt{(a - 4)^2} = |a - 4| = a - 4$
$\sqrt{(a - 11)^2} = |a - 11| = 11 - a$
则$\sqrt{(a - 4)^2} - \sqrt{(a - 11)^2} = (a - 4) - (11 - a) = a - 4 - 11 + a = 2a - 15$
答案:C
因为$a < 10 < 11$,所以$a - 4 > 0$,$a - 11 < 0$。
$\sqrt{(a - 4)^2} = |a - 4| = a - 4$
$\sqrt{(a - 11)^2} = |a - 11| = 11 - a$
则$\sqrt{(a - 4)^2} - \sqrt{(a - 11)^2} = (a - 4) - (11 - a) = a - 4 - 11 + a = 2a - 15$
答案:C
3. (泰州中考)下列各组二次根式中,化简后被开方数相同的是 (
A.$\sqrt {8}与\sqrt {3}$
B.$\sqrt {2}与\sqrt {12}$
C.$\sqrt {5}与\sqrt {15}$
D.$\sqrt {75}与\sqrt {27}$
D
)A.$\sqrt {8}与\sqrt {3}$
B.$\sqrt {2}与\sqrt {12}$
C.$\sqrt {5}与\sqrt {15}$
D.$\sqrt {75}与\sqrt {27}$
答案:
解:
A. $\sqrt{8}=2\sqrt{2}$,被开方数为2;$\sqrt{3}$被开方数为3,不同。
B. $\sqrt{12}=2\sqrt{3}$,被开方数为3;$\sqrt{2}$被开方数为2,不同。
C. $\sqrt{5}$与$\sqrt{15}$被开方数分别为5和15,不同。
D. $\sqrt{75}=5\sqrt{3}$,$\sqrt{27}=3\sqrt{3}$,被开方数均为3,相同。
答案:D
A. $\sqrt{8}=2\sqrt{2}$,被开方数为2;$\sqrt{3}$被开方数为3,不同。
B. $\sqrt{12}=2\sqrt{3}$,被开方数为3;$\sqrt{2}$被开方数为2,不同。
C. $\sqrt{5}$与$\sqrt{15}$被开方数分别为5和15,不同。
D. $\sqrt{75}=5\sqrt{3}$,$\sqrt{27}=3\sqrt{3}$,被开方数均为3,相同。
答案:D
4. 下列计算中,错误的是 (
A.$6\sqrt {2}×\sqrt {3}= 6\sqrt {6}$
B.$\sqrt {27}÷\sqrt {3}= 3$
C.$\sqrt {32}-\sqrt {2}= 3\sqrt {2}$
D.$(\sqrt {2}-\sqrt {3})×(\sqrt {2}+\sqrt {3})= 1$
D
)A.$6\sqrt {2}×\sqrt {3}= 6\sqrt {6}$
B.$\sqrt {27}÷\sqrt {3}= 3$
C.$\sqrt {32}-\sqrt {2}= 3\sqrt {2}$
D.$(\sqrt {2}-\sqrt {3})×(\sqrt {2}+\sqrt {3})= 1$
答案:
解:
A. $6\sqrt{2}×\sqrt{3}=6\sqrt{2×3}=6\sqrt{6}$,正确;
B. $\sqrt{27}÷\sqrt{3}=\sqrt{27÷3}=\sqrt{9}=3$,正确;
C. $\sqrt{32}-\sqrt{2}=4\sqrt{2}-\sqrt{2}=3\sqrt{2}$,正确;
D. $(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})=(\sqrt{2})^2-(\sqrt{3})^2=2-3=-1≠1$,错误。
答案:D
A. $6\sqrt{2}×\sqrt{3}=6\sqrt{2×3}=6\sqrt{6}$,正确;
B. $\sqrt{27}÷\sqrt{3}=\sqrt{27÷3}=\sqrt{9}=3$,正确;
C. $\sqrt{32}-\sqrt{2}=4\sqrt{2}-\sqrt{2}=3\sqrt{2}$,正确;
D. $(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})=(\sqrt{2})^2-(\sqrt{3})^2=2-3=-1≠1$,错误。
答案:D
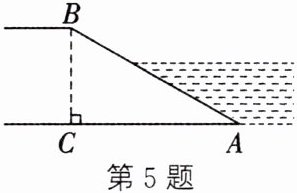
5. 如图,河坝横断面迎水坡AB的坡比为$1:\sqrt {3}$,坝高BC为4m,则AB的长为 (
A.$4\sqrt {3}m$
B.8m
C.$8\sqrt {3}m$
D.16m
B
) 
A.$4\sqrt {3}m$
B.8m
C.$8\sqrt {3}m$
D.16m
答案:
解:
∵迎水坡AB的坡比为$1:\sqrt{3}$,
∴$\frac{BC}{AC}=\frac{1}{\sqrt{3}}$。
∵BC=4m,
∴$AC=4\sqrt{3}m$。
在Rt△ABC中,
$AB=\sqrt{BC^{2}+AC^{2}}=\sqrt{4^{2}+(4\sqrt{3})^{2}}=\sqrt{16 + 48}=\sqrt{64}=8m$。
答案:B
∵迎水坡AB的坡比为$1:\sqrt{3}$,
∴$\frac{BC}{AC}=\frac{1}{\sqrt{3}}$。
∵BC=4m,
∴$AC=4\sqrt{3}m$。
在Rt△ABC中,
$AB=\sqrt{BC^{2}+AC^{2}}=\sqrt{4^{2}+(4\sqrt{3})^{2}}=\sqrt{16 + 48}=\sqrt{64}=8m$。
答案:B
6. (恩施中考)从$\sqrt {2},-\sqrt {3},-\sqrt {2}$这三个数中任选两个数相乘,所有乘积中小于2的有 (
A.0个
B.1个
C.2个
D.3个
C
)A.0个
B.1个
C.2个
D.3个
答案:
解:从三个数中任选两个数相乘,有以下三种情况:
1. $\sqrt{2} × (-\sqrt{3}) = -\sqrt{6} \approx -2.45 < 2$
2. $\sqrt{2} × (-\sqrt{2}) = -(\sqrt{2} × \sqrt{2}) = -2 < 2$
3. $(-\sqrt{3}) × (-\sqrt{2}) = \sqrt{6} \approx 2.45 > 2$
其中小于2的乘积有2个。
C
1. $\sqrt{2} × (-\sqrt{3}) = -\sqrt{6} \approx -2.45 < 2$
2. $\sqrt{2} × (-\sqrt{2}) = -(\sqrt{2} × \sqrt{2}) = -2 < 2$
3. $(-\sqrt{3}) × (-\sqrt{2}) = \sqrt{6} \approx 2.45 > 2$
其中小于2的乘积有2个。
C
7. 新情境 游戏活动 老师设计了接力游戏,用合作的方式完成二次根式的运算,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简,过程如图所示. 接力中,自己负责的一步出现错误的是 (
A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
A
)A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
答案:
A
8. 若要在$(5\sqrt {2}-\sqrt {2})□\sqrt {2}$的“□”中填上一个运算符号,使计算结果最大,则这个运算符号是 (
A.+
B.-
C.×
D.÷
C
)A.+
B.-
C.×
D.÷
答案:
1. 首先计算$(5\sqrt{2}-\sqrt{2})$的值:
$5\sqrt{2}-\sqrt{2}=(5 - 1)\sqrt{2}=4\sqrt{2}$。
2. 然后分别计算填入不同运算符号时的结果:
当填入“$+$”时:
结果为$4\sqrt{2}+\sqrt{2}=(4 + 1)\sqrt{2}=5\sqrt{2}\approx5×1.414 = 7.07$。
当填入“$-$”时:
结果为$4\sqrt{2}-\sqrt{2}=(4 - 1)\sqrt{2}=3\sqrt{2}\approx3×1.414 = 4.242$。
当填入“$×$”时:
结果为$4\sqrt{2}×\sqrt{2}=4×(\sqrt{2}×\sqrt{2})=4×2 = 8$。
当填入“$÷$”时:
结果为$4\sqrt{2}÷\sqrt{2}=4$。
3. 最后比较结果大小:
因为$8>5\sqrt{2}>4>3\sqrt{2}$。
所以这个运算符号是“$×$”,答案是C。
$5\sqrt{2}-\sqrt{2}=(5 - 1)\sqrt{2}=4\sqrt{2}$。
2. 然后分别计算填入不同运算符号时的结果:
当填入“$+$”时:
结果为$4\sqrt{2}+\sqrt{2}=(4 + 1)\sqrt{2}=5\sqrt{2}\approx5×1.414 = 7.07$。
当填入“$-$”时:
结果为$4\sqrt{2}-\sqrt{2}=(4 - 1)\sqrt{2}=3\sqrt{2}\approx3×1.414 = 4.242$。
当填入“$×$”时:
结果为$4\sqrt{2}×\sqrt{2}=4×(\sqrt{2}×\sqrt{2})=4×2 = 8$。
当填入“$÷$”时:
结果为$4\sqrt{2}÷\sqrt{2}=4$。
3. 最后比较结果大小:
因为$8>5\sqrt{2}>4>3\sqrt{2}$。
所以这个运算符号是“$×$”,答案是C。
9. 对于任意的正数m,n,定义运算“※”:$m※n= \left\{\begin{array}{l} \sqrt {m}-\sqrt {n}(m≥n),\\ \sqrt {m}+\sqrt {n}(m<n).\end{array} \right. $
计算$(3※2)×(8※12)$的结果为 (
A.$2-4\sqrt {6}$
B.2
C.$2\sqrt {5}$
D.20
计算$(3※2)×(8※12)$的结果为 (
B
)A.$2-4\sqrt {6}$
B.2
C.$2\sqrt {5}$
D.20
答案:
1. 首先计算$3※2$:
因为$3\gt2$,根据定义$m※n = \left\{\begin{array}{l}\sqrt{m}-\sqrt{n}(m\geq n)\\\sqrt{m}+\sqrt{n}(m\lt n)\end{array}\right.$,这里$m = 3$,$n = 2$。
所以$3※2=\sqrt{3}-\sqrt{2}$。
2. 然后计算$8※12$:
因为$8\lt12$,这里$m = 8$,$n = 12$。
所以$8※12=\sqrt{8}+\sqrt{12}$。
化简$\sqrt{8}+\sqrt{12}$:
根据$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}(a\geq0,b\geq0)$,$\sqrt{8}=\sqrt{4×2}=2\sqrt{2}$,$\sqrt{12}=\sqrt{4×3}=2\sqrt{3}$。
则$8※12 = 2\sqrt{2}+2\sqrt{3}$。
3. 最后计算$(3※2)×(8※12)$:
$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})$。
根据乘法分配律$(a - b)(c + d)=ac+ad - bc - bd$,这里$a=\sqrt{3}$,$b = \sqrt{2}$,$c = 2\sqrt{2}$,$d = 2\sqrt{3}$。
则$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})=\sqrt{3}×2\sqrt{2}+\sqrt{3}×2\sqrt{3}-\sqrt{2}×2\sqrt{2}-\sqrt{2}×2\sqrt{3}$。
计算各项:
$\sqrt{3}×2\sqrt{2}=2\sqrt{6}$;$\sqrt{3}×2\sqrt{3}=2×3 = 6$;$\sqrt{2}×2\sqrt{2}=2×2 = 4$;$\sqrt{2}×2\sqrt{3}=2\sqrt{6}$。
所以$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})=2\sqrt{6}+6 - 4-2\sqrt{6}$。
合并同类项:$(2\sqrt{6}-2\sqrt{6})+(6 - 4)=2$。
所以$(3※2)×(8※12)$的结果为$2$,答案是B。
因为$3\gt2$,根据定义$m※n = \left\{\begin{array}{l}\sqrt{m}-\sqrt{n}(m\geq n)\\\sqrt{m}+\sqrt{n}(m\lt n)\end{array}\right.$,这里$m = 3$,$n = 2$。
所以$3※2=\sqrt{3}-\sqrt{2}$。
2. 然后计算$8※12$:
因为$8\lt12$,这里$m = 8$,$n = 12$。
所以$8※12=\sqrt{8}+\sqrt{12}$。
化简$\sqrt{8}+\sqrt{12}$:
根据$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}(a\geq0,b\geq0)$,$\sqrt{8}=\sqrt{4×2}=2\sqrt{2}$,$\sqrt{12}=\sqrt{4×3}=2\sqrt{3}$。
则$8※12 = 2\sqrt{2}+2\sqrt{3}$。
3. 最后计算$(3※2)×(8※12)$:
$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})$。
根据乘法分配律$(a - b)(c + d)=ac+ad - bc - bd$,这里$a=\sqrt{3}$,$b = \sqrt{2}$,$c = 2\sqrt{2}$,$d = 2\sqrt{3}$。
则$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})=\sqrt{3}×2\sqrt{2}+\sqrt{3}×2\sqrt{3}-\sqrt{2}×2\sqrt{2}-\sqrt{2}×2\sqrt{3}$。
计算各项:
$\sqrt{3}×2\sqrt{2}=2\sqrt{6}$;$\sqrt{3}×2\sqrt{3}=2×3 = 6$;$\sqrt{2}×2\sqrt{2}=2×2 = 4$;$\sqrt{2}×2\sqrt{3}=2\sqrt{6}$。
所以$(\sqrt{3}-\sqrt{2})(2\sqrt{2}+2\sqrt{3})=2\sqrt{6}+6 - 4-2\sqrt{6}$。
合并同类项:$(2\sqrt{6}-2\sqrt{6})+(6 - 4)=2$。
所以$(3※2)×(8※12)$的结果为$2$,答案是B。
10. 在一个大正方形上,按如图所示的方式粘贴面积分别为12,10的两个小正方形,粘贴后,这两个小正方形重合部分的面积为3,则空白部分的面积为 (
A.8
B.19
C.$6\sqrt {7}$
D.$2\sqrt {30}-6$
D
)A.8
B.19
C.$6\sqrt {7}$
D.$2\sqrt {30}-6$
答案:
1. 首先,设大正方形的边长为$a$,面积为$12$的小正方形边长为$b$,面积为$10$的小正方形边长为$c$:
根据正方形面积公式$S = x^{2}$($S$为面积,$x$为边长),由$S_1=b^{2}=12$,$S_2 = c^{2}=10$,重合部分面积$S_0 = 3$。
大正方形的面积$S=a^{2}=(b + c-\sqrt{S_0})^{2}$(根据图形的边长关系,大正方形边长等于两个小正方形边长之和减去重合部分的边长)。
根据完全平方公式$(m + n - p)^{2}=m^{2}+n^{2}+p^{2}+2mn-2mp - 2np$,这里$m = b$,$n = c$,$p=\sqrt{S_0}$,则$a^{2}=b^{2}+c^{2}+S_0+2bc-2b\sqrt{S_0}-2c\sqrt{S_0}$。
空白部分面积$S_{空白}=a^{2}-b^{2}-c^{2}+S_0$(空白部分面积等于大正方形面积减去两个小正方形面积再加上重合部分面积,因为两个小正方形面积和多减了一次重合部分面积)。
把$a^{2}=(b + c-\sqrt{S_0})^{2}$代入$S_{空白}$得:$S_{空白}=(b + c-\sqrt{S_0})^{2}-b^{2}-c^{2}+S_0$。
展开$(b + c-\sqrt{S_0})^{2}$:
$(b + c-\sqrt{S_0})^{2}=b^{2}+c^{2}+S_0 + 2bc-2b\sqrt{S_0}-2c\sqrt{S_0}$。
所以$S_{空白}=b^{2}+c^{2}+S_0 + 2bc-2b\sqrt{S_0}-2c\sqrt{S_0}-b^{2}-c^{2}+S_0$。
化简得$S_{空白}=2S_0+2bc-2\sqrt{S_0}(b + c)$。
另一种方法:
大正方形的面积$S=( \sqrt{12}+\sqrt{10}-\sqrt{3})^{2}$。
根据完全平方公式$(x + y - z)^{2}=x^{2}+y^{2}+z^{2}+2xy-2xz - 2yz$,这里$x=\sqrt{12}$,$y = \sqrt{10}$,$z=\sqrt{3}$。
则$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=12 + 10+3+2\sqrt{12×10}-2\sqrt{12×3}-2\sqrt{10×3}$。
计算$2\sqrt{12×10}-2\sqrt{12×3}-2\sqrt{10×3}=4\sqrt{30}-12 - 2\sqrt{30}=2\sqrt{30}-12$,$12 + 10+3=25$,所以$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=25+2\sqrt{30}-12=13 + 2\sqrt{30}$。
空白部分面积$S_{空白}=(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}-12 - 10+3$。
把$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=13 + 2\sqrt{30}$代入得:$S_{空白}=13 + 2\sqrt{30}-12 - 10+3$。
还有一种更简单的思路:
空白部分面积$S_{空白}=( \sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})$(通过对图形进行分割,利用边长关系,空白部分可看作两个长方形面积之和,一个长方形长为$\sqrt{12}-\sqrt{3}$,宽为$\sqrt{10}-\sqrt{3}$)。
根据多项式乘法法则$(m - n)(p - q)=mp-mq - np+nq$,这里$m=\sqrt{12}$,$n=\sqrt{3}$,$p=\sqrt{10}$,$q=\sqrt{3}$。
则$(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})=\sqrt{12×10}-\sqrt{12×3}-\sqrt{10×3}+3$。
因为$\sqrt{12×10}=2\sqrt{30}$,$\sqrt{12×3}=6$,$\sqrt{10×3}=\sqrt{30}$。
所以$(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})=2\sqrt{30}-6-\sqrt{30}+3=\sqrt{30}-3$(错误),重新计算:
空白部分面积$S_{空白}=(\sqrt{12}-\sqrt{3})×(\sqrt{10}-\sqrt{3})+(\sqrt{12}-\sqrt{3})×(\sqrt{10}-\sqrt{3})$(从图形看,空白部分是两个相同的长方形)。
先计算一个长方形面积$S_1=(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})$,$S_1=\sqrt{12×10}-\sqrt{12×3}-\sqrt{10×3}+3=2\sqrt{30}-6 - \sqrt{30}+3=\sqrt{30}-3$(错误),正确的:
大正方形边长$a=\sqrt{12}+\sqrt{10}-\sqrt{3}$,大正方形面积$S=a^{2}=(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=12 + 10+3+2\sqrt{120}-2\sqrt{36}-2\sqrt{30}=25 + 4\sqrt{30}-12 - 2\sqrt{30}=13 + 2\sqrt{30}$。
空白部分面积$S_{空白}=13 + 2\sqrt{30}-12 - 10+3$(大正方形面积$-$两个小正方形面积$+$重合部分面积)。
$S_{空白}=2\sqrt{30}-6$。
所以空白部分的面积为$2\sqrt{30}-6$,答案是D。
根据正方形面积公式$S = x^{2}$($S$为面积,$x$为边长),由$S_1=b^{2}=12$,$S_2 = c^{2}=10$,重合部分面积$S_0 = 3$。
大正方形的面积$S=a^{2}=(b + c-\sqrt{S_0})^{2}$(根据图形的边长关系,大正方形边长等于两个小正方形边长之和减去重合部分的边长)。
根据完全平方公式$(m + n - p)^{2}=m^{2}+n^{2}+p^{2}+2mn-2mp - 2np$,这里$m = b$,$n = c$,$p=\sqrt{S_0}$,则$a^{2}=b^{2}+c^{2}+S_0+2bc-2b\sqrt{S_0}-2c\sqrt{S_0}$。
空白部分面积$S_{空白}=a^{2}-b^{2}-c^{2}+S_0$(空白部分面积等于大正方形面积减去两个小正方形面积再加上重合部分面积,因为两个小正方形面积和多减了一次重合部分面积)。
把$a^{2}=(b + c-\sqrt{S_0})^{2}$代入$S_{空白}$得:$S_{空白}=(b + c-\sqrt{S_0})^{2}-b^{2}-c^{2}+S_0$。
展开$(b + c-\sqrt{S_0})^{2}$:
$(b + c-\sqrt{S_0})^{2}=b^{2}+c^{2}+S_0 + 2bc-2b\sqrt{S_0}-2c\sqrt{S_0}$。
所以$S_{空白}=b^{2}+c^{2}+S_0 + 2bc-2b\sqrt{S_0}-2c\sqrt{S_0}-b^{2}-c^{2}+S_0$。
化简得$S_{空白}=2S_0+2bc-2\sqrt{S_0}(b + c)$。
另一种方法:
大正方形的面积$S=( \sqrt{12}+\sqrt{10}-\sqrt{3})^{2}$。
根据完全平方公式$(x + y - z)^{2}=x^{2}+y^{2}+z^{2}+2xy-2xz - 2yz$,这里$x=\sqrt{12}$,$y = \sqrt{10}$,$z=\sqrt{3}$。
则$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=12 + 10+3+2\sqrt{12×10}-2\sqrt{12×3}-2\sqrt{10×3}$。
计算$2\sqrt{12×10}-2\sqrt{12×3}-2\sqrt{10×3}=4\sqrt{30}-12 - 2\sqrt{30}=2\sqrt{30}-12$,$12 + 10+3=25$,所以$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=25+2\sqrt{30}-12=13 + 2\sqrt{30}$。
空白部分面积$S_{空白}=(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}-12 - 10+3$。
把$(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=13 + 2\sqrt{30}$代入得:$S_{空白}=13 + 2\sqrt{30}-12 - 10+3$。
还有一种更简单的思路:
空白部分面积$S_{空白}=( \sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})$(通过对图形进行分割,利用边长关系,空白部分可看作两个长方形面积之和,一个长方形长为$\sqrt{12}-\sqrt{3}$,宽为$\sqrt{10}-\sqrt{3}$)。
根据多项式乘法法则$(m - n)(p - q)=mp-mq - np+nq$,这里$m=\sqrt{12}$,$n=\sqrt{3}$,$p=\sqrt{10}$,$q=\sqrt{3}$。
则$(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})=\sqrt{12×10}-\sqrt{12×3}-\sqrt{10×3}+3$。
因为$\sqrt{12×10}=2\sqrt{30}$,$\sqrt{12×3}=6$,$\sqrt{10×3}=\sqrt{30}$。
所以$(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})=2\sqrt{30}-6-\sqrt{30}+3=\sqrt{30}-3$(错误),重新计算:
空白部分面积$S_{空白}=(\sqrt{12}-\sqrt{3})×(\sqrt{10}-\sqrt{3})+(\sqrt{12}-\sqrt{3})×(\sqrt{10}-\sqrt{3})$(从图形看,空白部分是两个相同的长方形)。
先计算一个长方形面积$S_1=(\sqrt{12}-\sqrt{3})(\sqrt{10}-\sqrt{3})$,$S_1=\sqrt{12×10}-\sqrt{12×3}-\sqrt{10×3}+3=2\sqrt{30}-6 - \sqrt{30}+3=\sqrt{30}-3$(错误),正确的:
大正方形边长$a=\sqrt{12}+\sqrt{10}-\sqrt{3}$,大正方形面积$S=a^{2}=(\sqrt{12}+\sqrt{10}-\sqrt{3})^{2}=12 + 10+3+2\sqrt{120}-2\sqrt{36}-2\sqrt{30}=25 + 4\sqrt{30}-12 - 2\sqrt{30}=13 + 2\sqrt{30}$。
空白部分面积$S_{空白}=13 + 2\sqrt{30}-12 - 10+3$(大正方形面积$-$两个小正方形面积$+$重合部分面积)。
$S_{空白}=2\sqrt{30}-6$。
所以空白部分的面积为$2\sqrt{30}-6$,答案是D。
查看更多完整答案,请扫码查看


