《2025年小题狂做高中数学必修第二册人教版巅峰版》

6. [多选题，2024湖南郴州期中]下列命题正确的是(CD)

A.若平面向量a，b，c两两的夹角相等，且|a|=|b|=|c|=2，则|a+b+c|的值为0
B.已知c≠0，且a·c=b·c，则a=b
C.若$\overrightarrow{AC}$·$\overrightarrow{AB}$＞$\overrightarrow{AB}$²，则△ABC为钝角三角形
D.已知点O为△ABC的外心，且|$\overrightarrow{AC}$|=4，|$\overrightarrow{AB}$|=2，则$\overrightarrow{AO}$·$\overrightarrow{BC}$=6

答案：
6.CD对于A，平面向量$a$，$b$，$c$两两的夹角相等，故夹角可能为$120^{\circ}$或$0^{\circ}$，若两两夹角为$0^{\circ}$，则$|a + b + c| = 6$，故A错误；对于B，由$a· c = b· c$，得$a· c - b· c = 0$，故$(a - b)· c = 0$，又$c\neq 0$，则$a = b$或$(a - b)\perp c$，故B错误；对于C，$\overrightarrow{BA}· \overrightarrow{BC}=-\overrightarrow{AB}· (\overrightarrow{AC}-\overrightarrow{AB})=-\overrightarrow{AB}· \overrightarrow{AC}+\overrightarrow{AB}^{2}=-(\overrightarrow{AB}· \overrightarrow{AC}-|\overrightarrow{AB}|^{2})＜0$，所以$\cos B=\frac{\overrightarrow{BA}· \overrightarrow{BC}}{|\overrightarrow{BA}|· |\overrightarrow{BC}|}＜0$，所以$\triangle ABC$为钝角三角形，故C正确；对于D，如图所示，$D$，$E$分别为$AC$，$AB$的中点，因为$O$为$\triangle ABC$的外心，且$|\overrightarrow{AC}| = 4$，$|\overrightarrow{AB}| = 2$，所以$AD = 2$，$AE = 1$，且$OD\perp AC$，$OE\perp AB$，由向量投影定义可知，$\overrightarrow{AO}· \overrightarrow{AC}=|\overrightarrow{AO}|· |\overrightarrow{AC}|· \cos\angle OAC=|\overrightarrow{AD}|· |\overrightarrow{AC}|=2× 4 = 8$，$\overrightarrow{AO}· \overrightarrow{AB}=|\overrightarrow{AO}|· |\overrightarrow{AB}|· \cos\angle OAB=|\overrightarrow{AE}|· |\overrightarrow{AB}|=1× 2 = 2$，
　　　　
则$\overrightarrow{AO}· \overrightarrow{BC}=\overrightarrow{AO}· (\overrightarrow{AC}-\overrightarrow{AB})=\overrightarrow{AO}· \overrightarrow{AC}-\overrightarrow{AO}· \overrightarrow{AB}=8 - 2 = 6$，D正确.

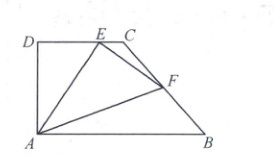
7. [2025浙江宁波荣安实验中学期末]如图，在直角梯形ABCD中，已知AB//CD，∠DAB=90°，AB=2AD=2CD=2，F是边BC上的中点，E是边CD上一个动点。则$\overrightarrow{EA}$·$\overrightarrow{EF}$的取值范围是$\left [ -\frac{1}{16},\frac{1}{2} \right ] $。

答案：
7.$\left [ -\frac{1}{16},\frac{1}{2} \right ] $建立如图所示的平面直角坐标系，设$\overrightarrow{DE}=\lambda \overrightarrow{DC}$，其中$0\leq\lambda\leq1$，则$A(0,0)$，$B(2,0)$，$C(1,1)$，$D(0,1)$，$F(\frac{3}{2},\frac{1}{2})$，$E(\lambda,1)$，则$\overrightarrow{EA}· \overrightarrow{EF}=(-\lambda, - 1)· (\frac{3}{2}-\lambda,-\frac{1}{2})=\lambda^{2}-\frac{3}{2}\lambda+\frac{1}{2}=(\lambda - \frac{3}{4})^{2}-\frac{1}{16}\in \left [ -\frac{1}{16},\frac{1}{2} \right ] $.
　　　　

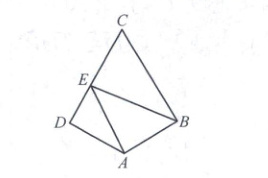
8. [2023江苏中华中学月考]如图，在平面四边形ABCD中，∠CDA=∠CBA=90°，∠BAD=120°，AB=AD=1。若E为边CD上的动点，则$\overrightarrow{AE}$·$\overrightarrow{BE}$的最小值为$\frac{21}{16}$。

答案：
8.$\frac{21}{16}$以$D$为原点，$DA$所在直线为$x$轴，$DC$所在直线为$y$轴，建立如图所示的平面直角坐标系，则$A(1,0)$，$B\left ( \frac{3}{2},\frac{\sqrt{3}}{2}\right ) $，$C(0,\sqrt{3})$.设点$E$的坐标为$(0,t)$，则$t\in [0,\sqrt{3}]$，所以$\overrightarrow{AE}=(-1,t)$，$\overrightarrow{BE}=\left ( -\frac{3}{2},t-\frac{\sqrt{3}}{2}\right ) $.所以$\overrightarrow{AE}· \overrightarrow{BE}=(-1,t)· \left ( -\frac{3}{2},t-\frac{\sqrt{3}}{2}\right ) =t^{2}-\frac{\sqrt{3}}{2}t+\frac{3}{2}=\left ( t-\frac{\sqrt{3}}{4}\right ) ^{2}+\frac{21}{16}$.所以当$t=\frac{\sqrt{3}}{4}$时，$(\overrightarrow{AE}· \overrightarrow{BE})_{\min}=\frac{21}{16}$.
　　　　　

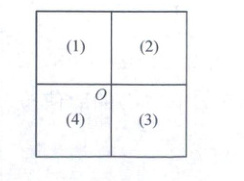
9. [2024浙江嘉兴中学期末]如图，将边长为1的大正方形分割成四个全等的小正方形，沿顺时针方向将小正方形依次记为(1)，(2)，(3)，(4)。P_i是小正方形(i)内部和边界上的动点(i=1，2，3，4)，O是大正方形的中心，则$\overrightarrow{OP_1}$·$\overrightarrow{OP_2}$+$\overrightarrow{OP_2}$·$\overrightarrow{OP_3}$+$\overrightarrow{OP_3}$·$\overrightarrow{OP_4}$+$\overrightarrow{OP_4}$·$\overrightarrow{OP_1}$的最小值是$-\frac{1}{2}$。

答案：
9.$-\frac{1}{2}$令$\overrightarrow{OP_{1}}+\overrightarrow{OP_{3}}=\overrightarrow{OA}$，$\overrightarrow{OP_{2}}+\overrightarrow{OP_{4}}=\overrightarrow{OB}$，所以$\overrightarrow{OP_{1}}· \overrightarrow{OP_{2}}+\overrightarrow{OP_{2}}· \overrightarrow{OP_{3}}+\overrightarrow{OP_{3}}· \overrightarrow{OP_{4}}+\overrightarrow{OP_{4}}· \overrightarrow{OP_{1}}=(\overrightarrow{OP_{1}}+\overrightarrow{OP_{3}})· (\overrightarrow{OP_{2}}+\overrightarrow{OP_{4}})=\overrightarrow{OA}· \overrightarrow{OB}=|\overrightarrow{OA}|· |\overrightarrow{OB}|· \cos\theta$.
如图，建立平面直角坐标系，设$P_{1}(x_{1},y_{1})$，$P_{3}(x_{3},y_{3})$，则$\overrightarrow{OP_{1}}+\overrightarrow{OP_{3}}=(x_{1}+x_{3},y_{1}+y_{3})=\overrightarrow{OA}$，因为$-\frac{1}{2}\leq x_{1}\leq 0$，$0\leq y_{1}\leq \frac{1}{2}$，$0\leq x_{3}\leq \frac{1}{2}$，$-\frac{1}{2}\leq y_{3}\leq 0$，所以$-\frac{1}{2}\leq x_{1}+x_{3}\leq \frac{1}{2}$，$-\frac{1}{2}\leq y_{1}+y_{3}\leq \frac{1}{2}$，所以$|\overrightarrow{OA}|=\sqrt{(x_{1}+x_{3})^{2}+(y_{1}+y_{3})^{2}}\leq \sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{2}}{2}$，当$\overrightarrow{OP_{1}}=(0,\frac{1}{2})$，$\overrightarrow{OP_{3}}=(\frac{1}{2},0)$或$\overrightarrow{OP_{1}}=(-\frac{1}{2},0)$，$\overrightarrow{OP_{3}}=(0,-\frac{1}{2})$或$\overrightarrow{OP_{1}}=(0,-\frac{1}{2})$，$\overrightarrow{OP_{3}}=(-\frac{1}{2},0)$时，等号成立，即$|\overrightarrow{OA}|$最大为$\frac{\sqrt{2}}{2}$.
同理，当$\overrightarrow{OP_{2}}=(0,0)$，$\overrightarrow{OP_{4}}=(-\frac{1}{2},-\frac{1}{2})$或$\overrightarrow{OP_{2}}=(\frac{1}{2},\frac{1}{2})$，$\overrightarrow{OP_{4}}=(0,0)$或$\overrightarrow{OP_{1}}=(-\frac{1}{2},\frac{1}{2})$，$\overrightarrow{OP_{3}}=(0,0)$，或$\overrightarrow{OP_{1}}=(0,0)$，$\overrightarrow{OP_{3}}=(\frac{1}{2},-\frac{1}{2})$，或$\overrightarrow{OP_{1}}=(-\frac{1}{2},0)$时，此时$|\overrightarrow{OA}|$最大为$\frac{\sqrt{2}}{2}$，$|\overrightarrow{OB}|$最大为$\frac{\sqrt{2}}{2}$.故当$\overrightarrow{OP_{1}}=(0,\frac{1}{2})$，$\overrightarrow{OP_{3}}=(\frac{1}{2},0)$，$\overrightarrow{OP_{2}}=(0,0)$，$\overrightarrow{OP_{4}}=(-\frac{1}{2},-\frac{1}{2})$，或$\overrightarrow{OP_{1}}=(-\frac{1}{2},0)$，$\overrightarrow{OP_{3}}=(0,-\frac{1}{2})$，或$\overrightarrow{OP_{1}}=(0,0)$，$\overrightarrow{OP_{3}}=(\frac{1}{2},-\frac{1}{2})$，$\overrightarrow{OP_{2}}=(\frac{1}{2},0)$时，此时$|\overrightarrow{OA}|$最大为$\frac{\sqrt{2}}{2}$，$|\overrightarrow{OB}|$最大为$\frac{\sqrt{2}}{2}$，且$\cos\theta = -1$，即$\overrightarrow{OP_{1}}· \overrightarrow{OP_{2}}+\overrightarrow{OP_{2}}· \overrightarrow{OP_{3}}+\overrightarrow{OP_{3}}· \overrightarrow{OP_{4}}+\overrightarrow{OP_{4}}· \overrightarrow{OP_{1}}$的最小值为$\frac{\sqrt{2}}{2}× \frac{\sqrt{2}}{2}× (-1)=-\frac{1}{2}$.