2025年小题狂做高中数学必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. [2025 天津河西期末]如图,在三棱台 $ ABC - A_{1}B_{1}C_{1} $中,截去三棱锥 $ A_{1} - ABC $,则剩余部分是 (
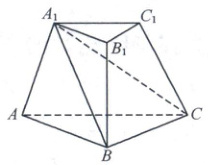
A.三棱锥
B.四棱锥
C.三棱柱
D.五棱锥
B
)
A.三棱锥
B.四棱锥
C.三棱柱
D.五棱锥
答案:
1.B 如图所示,在三棱台$A_{1}B_{1}C_{1}-ABC$中,沿$A_{1}BC$截去三棱锥$A_{1}-ABC$,剩余部分是四棱锥$A_{1}-BCC_{1}B_{1}$.

1.B 如图所示,在三棱台$A_{1}B_{1}C_{1}-ABC$中,沿$A_{1}BC$截去三棱锥$A_{1}-ABC$,剩余部分是四棱锥$A_{1}-BCC_{1}B_{1}$.

2. [2024 湖南娄底期末]在半径为 2 的球中挖去一个半径为 1 的同心球,设过球心的截面的面积为 $ S_{1} $,不过球心的任意非圆面的截面的面积为 $ S_{2} $,则 (
A.$ S_{1} = S_{2} $
B.$ S_{1} > S_{2} $
C.$ S_{1} < S_{2} $
D.$ S_{1},S_{2} $的大小关系不定
A
)A.$ S_{1} = S_{2} $
B.$ S_{1} > S_{2} $
C.$ S_{1} < S_{2} $
D.$ S_{1},S_{2} $的大小关系不定
答案:
2.A 过球心的截面为一个圆环,外半径为2,内半径为1,其面积$S_{1}=\pi(2^{2}-1^{2})=3\pi$.设球心到不过球心的任意非圆面的截面的距离为$d$,则该截面的面积$S_{2}=\pi[(2^{2}-d^{2})-(1^{2}-d^{2})]=3\pi$,所以$S_{1}=S_{2}$.
3. [数学文化,2025 湖北襄阳期末]如图,何尊是我国西周早期的青铜礼器,其造型浑厚,工艺精美,尊内底铸铭文中的“宅兹中国”为“中国”一词最早的文字记载,何尊还是第一个出现“德”字的器物,证明了周王朝以德治国的理念.何尊的形状可近似看作是由上部分圆台和下部分圆柱的组合体,组合体的高约为 40 cm,上口直径约为 28 cm,圆柱的底面直径约为 18 cm.取 $ \pi $的近似值为 3,经计算得到圆柱的侧面积约为 $ 1296 cm^{2} $,则该组合体上部分圆台的体积约为 (

A.$ 6448 cm^{3} $
B.$ 6548 cm^{3} $
C.$ 5548 cm^{3} $
D.$ 5448 cm^{3} $
A
)
A.$ 6448 cm^{3} $
B.$ 6548 cm^{3} $
C.$ 5548 cm^{3} $
D.$ 5448 cm^{3} $
答案:
3.A 由题意可知,该几何体上部分圆台的下底面半径$r_{1}=14\mathrm{cm}$,上底面半径$r_{2}=9\mathrm{cm}$,该几何体下部分圆柱的底面半径$r_{3}=9\mathrm{cm}$.设圆台的高为$h\mathrm{cm}$,则圆柱的高为$(40 - h)\mathrm{cm}$,则有$2\pi r_{3}(40 - h)=1296$,又$\pi$的近似值为3,所以$2×3×9×(40 - h)=1296$,解得$h = 16$,所以圆台的体积$V=\frac{1}{3}\pi(r_{1}^{2}+r_{2}^{2}+r_{1}r_{2})h\approx\frac{1}{3}×3×(14^{2}+9^{2}+14×9)×16 = 6448(\mathrm{cm}^{3})$.
4. [阅读信息,2025 陕西汉中中学期末]某餐厅为了追求时间效率,推出一种液体“沙漏”免单方案(即点单完成后,开始倒转“沙漏”,“沙漏”漏完前,客人所点的菜需全部上桌,否则该桌免费用餐).“沙漏”是由一个圆锥体和一个四棱柱相通连接而成.某次计时前如图 1 所示,已知圆锥体底面半径是 6 cm,高是 6.75 cm;四棱柱底面边长为 6 cm 和 $ 2\pi cm $,液体高是 6.5 cm.计时结束后如图 2 所示,则此时“沙漏”中液体的高度为 (
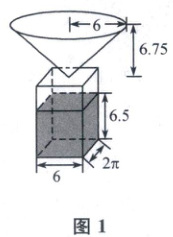
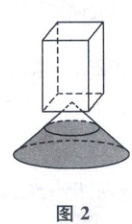
A.2 cm
B.3 cm
C.4 cm
D.4.5 cm
D
)

A.2 cm
B.3 cm
C.4 cm
D.4.5 cm
答案:
4.D 如图,圆锥的底面半径是$6\mathrm{cm}$,高是$6.75\mathrm{cm}$,所以$\triangle ABC$,$\triangle CDE$是直角三角形,由已知可得液体的体积为$6×2\pi×6.5 = 78\pi(\mathrm{cm}^{3})$,圆锥的体积为$\frac{1}{3}\pi×6^{2}×6.75 = 81\pi(\mathrm{cm}^{3})$,计时结束后,圆锥中没有液体的部分体积为$81\pi - 78\pi = 3\pi(\mathrm{cm}^{3})$.设计时结束后,“沙漏”中液体的高度$AD$为$x\mathrm{cm}$,则$\frac{3\pi}{81\pi}=(\frac{6.75 - x}{6.75})^{3}$,即$(\frac{6.75 - x}{6.75})^{3}=\frac{1}{27}$,所以$\frac{6.75 - x}{6.75}=\frac{1}{3}$,即$6.75 - x = 2.25$,解得$x = 4.5$,所以计时结束后,“沙漏”中液体的高度为$4.5\mathrm{cm}$.

4.D 如图,圆锥的底面半径是$6\mathrm{cm}$,高是$6.75\mathrm{cm}$,所以$\triangle ABC$,$\triangle CDE$是直角三角形,由已知可得液体的体积为$6×2\pi×6.5 = 78\pi(\mathrm{cm}^{3})$,圆锥的体积为$\frac{1}{3}\pi×6^{2}×6.75 = 81\pi(\mathrm{cm}^{3})$,计时结束后,圆锥中没有液体的部分体积为$81\pi - 78\pi = 3\pi(\mathrm{cm}^{3})$.设计时结束后,“沙漏”中液体的高度$AD$为$x\mathrm{cm}$,则$\frac{3\pi}{81\pi}=(\frac{6.75 - x}{6.75})^{3}$,即$(\frac{6.75 - x}{6.75})^{3}=\frac{1}{27}$,所以$\frac{6.75 - x}{6.75}=\frac{1}{3}$,即$6.75 - x = 2.25$,解得$x = 4.5$,所以计时结束后,“沙漏”中液体的高度为$4.5\mathrm{cm}$.

5. [多选题,2024 安徽六安月考]用一张长为 8,宽为 4 的矩形硬纸卷成圆柱的侧面,则相应圆柱的底面半径可以是 (
A.2
B.$ 2\pi $
C.$ \frac{2}{\pi} $
D.$ \frac{4}{\pi} $
CD
)A.2
B.$ 2\pi $
C.$ \frac{2}{\pi} $
D.$ \frac{4}{\pi} $
答案:
5.CD 如图,设圆柱的底面半径为$r$,若矩形的长为卷成圆柱底面的周长,则$2\pi r = 8$,所以$r=\frac{4}{\pi}$;同理,若矩形的宽为卷成圆柱底面的周长,则$2\pi r = 4$,所以$r=\frac{2}{\pi}$.

5.CD 如图,设圆柱的底面半径为$r$,若矩形的长为卷成圆柱底面的周长,则$2\pi r = 8$,所以$r=\frac{4}{\pi}$;同理,若矩形的宽为卷成圆柱底面的周长,则$2\pi r = 4$,所以$r=\frac{2}{\pi}$.

6. [多选题,2024 湖北襄阳期末]绿水青山就是金山银山,为响应党的号召,某小区把一处荒地改造成公园进行绿化.在绿化带旁边放置一些砌成的完全相同的石墩,石墩的上部是半径为 15 cm 的球的一部分,下部是底面半径为 12 cm 的圆柱体,整个石墩的高为 48 cm,如图所示(注:球体被平面所截,截得的部分叫球缺,球缺表面上的点到截面的最大距离为球缺的高.球缺的体积 $ V = \frac{1}{3}\pi(3R - h) · h^{2} $,其中 $ R $为球的半径,$ h $为球缺的高),则下列说法正确的是 (
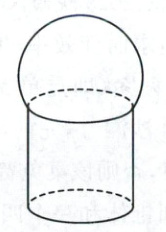
A.石墩上、下两部分的高之比为 $ 1:1 $
B.石墩表面上两点间距离的最大值为 $ (6\sqrt{30} + 15) $cm
C.每个石墩的体积为 $ 7488\pi cm^{3} $
D.将石墩放置在一个球内,则该球的半径的最小值为 $ \frac{51}{2} $cm
ACD
)
A.石墩上、下两部分的高之比为 $ 1:1 $
B.石墩表面上两点间距离的最大值为 $ (6\sqrt{30} + 15) $cm
C.每个石墩的体积为 $ 7488\pi cm^{3} $
D.将石墩放置在一个球内,则该球的半径的最小值为 $ \frac{51}{2} $cm
答案:
6.ACD 如图1,设球缺的球心为$O$,过点$O$作$OF\perp DC$,垂足为$F$,交$AB$于点$E$,由已知可得半径$R = 15\mathrm{cm}$,$AE=\frac{1}{2}AB = 12\mathrm{cm}$,所以$OE=\sqrt{OA^{2}-AE^{2}}=\sqrt{15^{2}-12^{2}} = 9(\mathrm{cm})$,如图2,延长$EO$与球缺交于点$S$,可得$SE = R + OE = 24(\mathrm{cm})$,则石墩上、下两部分的高之比为$24:24 = 1:1$,故A正确;连接$OC$,则$OC=\sqrt{OF^{2}+FC^{2}}=\sqrt{33^{2}+12^{2}} = 3\sqrt{137}\mathrm{cm}$,所以石墩表面上两点间距离的最大值为$OC + R=(3\sqrt{137}+15)\mathrm{cm}$,故B错误;由前面的计算可知上部分球缺的高$h = 24\mathrm{cm}$,所以石墩的体积$V=\frac{1}{3}\pi(3×15 - 24)×24^{2}+\pi×12^{2}×24 = 7488\pi\mathrm{cm}^{3}$,故C正确;设该球的半径为$r$,则$(48 - r)^{2}+12^{2}=r^{2}$,解得$r=\frac{51}{2}\mathrm{cm}$,故D正确.


6.ACD 如图1,设球缺的球心为$O$,过点$O$作$OF\perp DC$,垂足为$F$,交$AB$于点$E$,由已知可得半径$R = 15\mathrm{cm}$,$AE=\frac{1}{2}AB = 12\mathrm{cm}$,所以$OE=\sqrt{OA^{2}-AE^{2}}=\sqrt{15^{2}-12^{2}} = 9(\mathrm{cm})$,如图2,延长$EO$与球缺交于点$S$,可得$SE = R + OE = 24(\mathrm{cm})$,则石墩上、下两部分的高之比为$24:24 = 1:1$,故A正确;连接$OC$,则$OC=\sqrt{OF^{2}+FC^{2}}=\sqrt{33^{2}+12^{2}} = 3\sqrt{137}\mathrm{cm}$,所以石墩表面上两点间距离的最大值为$OC + R=(3\sqrt{137}+15)\mathrm{cm}$,故B错误;由前面的计算可知上部分球缺的高$h = 24\mathrm{cm}$,所以石墩的体积$V=\frac{1}{3}\pi(3×15 - 24)×24^{2}+\pi×12^{2}×24 = 7488\pi\mathrm{cm}^{3}$,故C正确;设该球的半径为$r$,则$(48 - r)^{2}+12^{2}=r^{2}$,解得$r=\frac{51}{2}\mathrm{cm}$,故D正确.


查看更多完整答案,请扫码查看


