《2025年小题狂做高中数学必修第二册人教版巅峰版》

20. [2022 全国甲卷理,7]在长方体 $ ABCD - A_1B_1C_1D_1 $ 中，已知 $ B_1D $ 与平面 $ ABCD $ 和平面 $ AA_1B_1B $ 所成的角均为 $ 30° $，则(D)

A.$ AB = 2AD $
B.$ AB $ 与平面 $ A_1B_1C_1D_1 $ 所成的角为 $ 30° $
C.$ AC = CB_1 $
D.$ B_1D $ 与平面 $ BB_1C_1C $ 所成的角为 $ 45° $

答案：
20.D　如图所示，因为在长方体ABCD - A₁B₁C₁D₁中，BB₁⊥平面ABCD，AD⊥平面AA₁B₁B，所以B₁D与平面ABCD所成角为∠B₁DB，B₁D与平面AA₁B₁B所成角为∠DB₁A，则∠B₁DB = ∠DB₁A = 30°。不妨设AB = a，AD = b，AA₁ = c，则sin30° = c/B₁D = b/B₁D，即b = c，B₁D = 2c = √(a² + b² + c²)，解得a = √2c。对于A，AB = a，AD = b，AB = √2AD，A错误；对于B，过点B作BE⊥AB₁于点E，因为在长方体ABCD - A₁B₁C₁D₁中，DA⊥平面AA₁B₁B，所以BE⊥AD，又AD∩AB₁ = A，AB₁，AD⊂平面AB₁D，所以BE⊥平面AB₁D，所以∠B₁AE为AB₁与平面AB₁D所成的角，从而tan∠B₁AE = c/a = √2/2，所以∠B₁AE≠30°，B错误；对于C，AC = √(a² + b²) = √3c，CB₁ = √(b² + c²) = √2c，AC≠CB₁，C错误；对于D，∠DB₁C为B₁D与平面BB₁CC₁所成角，则sin∠DB₁C = CD/B₁D = a/2c = √2/2，而0°＜∠DB₁C＜90°，所以∠DB₁C = 45°，D正确。

21. [2022 全国甲卷理,9]甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为 $ 2\pi $，侧面积分别为 $ S_{甲} $ 和 $ S_{乙} $，体积分别为 $ V_{甲} $ 和 $ V_{乙} $，若 $ \frac{S_{甲}}{S_{乙}} = 2 $，则 $ \frac{V_{甲}}{V_{乙}} = $(C)

A.$ \sqrt{5} $
B.$ 2\sqrt{2} $
C.$ \sqrt{10} $
D.$ \frac{5\sqrt{10}}{4} $

答案： 21.C　设母线长为l，甲圆锥底面半径为r₁，乙圆锥底面圆半径为r₂，则S₁/S₂ = (πr₁l)/(πr₂l) = r₁/r₂ = 2，所以r₁ = 2r₂，又2πr₁/l + 2πr₂/l = 2π，则r₁ + r₂ = l，所以r₁ = 2/3l，r₂ = 1/3l，所以甲圆锥的高h₁ = √[l² - (2/3l)²] = √5/3l，乙圆锥的高h₂ = √[l² - (1/3l)²] = 2√2/3l，所以V₁/V₂ = (1/3πr₁²h₁)/(1/3πr₂²h₂) = (4/9l²×√5/3l)/(1/9l²×2√2/3l) = √10/2。

22. [2024 新高考Ⅱ卷,7]已知正三棱台 $ ABC - A_1B_1C_1 $ 的体积为 $ \frac{52}{3} $，$ AB = 6 $，$ A_1B_1 = 2 $，则 $ A_1A $ 与平面 $ ABC $ 所成角的正切值为()

A.$ \frac{1}{2} $
B.$ 1 $
C.$ 2 $
D.$ 3 $

答案： B

23. [多选题,2023 新高考Ⅰ卷,12]下列物体中，能够被整体放入棱长为 1(单位：m)的正方体容器(容器壁厚度忽略不计)内的有(ABD)

A.直径为 $ 0.99 m $ 的球体
B.所有棱长均为 $ 1.4 m $ 的四面体
C.底面直径为 $ 0.01 m $，高为 $ 1.8 m $ 的圆柱体
D.底面直径为 $ 1.2 m $，高为 $ 0.01 m $ 的圆柱体

答案：
23.ABD　对于A，由于球的直径为0.99m，小于正方体的棱长1m，故球体可以放入正方体容器内，故A正确；对于B，如图，连接正方体的面对角线，得正四面体A₁ - BC₁D，则它的棱长为√2＞1.4，故B正确；对于C，由于正方体的体对角线长为√3＜1.8，故C错误；对于D，由于高为0.01m，可忽略不计，看作直径为1.2m的平面图形，E，F，G，H，I，J为各棱中点，六边形EFGHIJ为正六边形，其边长为√2/2m，其内切圆直径为FH，所以FH = √3FG = √6/2m，因为(√6/2)² = 3/2＞1.2²，故D正确。

24. [2020 新高考全国Ⅰ卷,16]已知直四棱柱 $ ABCD - A_1B_1C_1D_1 $ 的棱长均为 2，$ \angle BAD = 60° $.以 $ D_1 $ 为球心，$ \sqrt{5} $ 为半径的球面与侧面 $ BCC_1B_1 $ 的交线为√2π/2.

答案：
24.√2π/2　如图所示的直四棱柱中，由题意知，△BCD₁是边长为2的等边三角形，取BC₁的中点O，连接D₁O，则D₁O⊥BC₁。又BB₁⊥底面A₁B₁C₁D₁，D₁O⊂底面A₁B₁C₁D₁，所以BB₁⊥D₁O，又B₁C₁∩BB₁ = B₁，B₁C₁，BB₁⊂平面BCC₁B₁，所以D₁O⊥平面BCC₁B₁。所以O为截面圆的圆心。又D₁O = √3，球的半径为√5，截面圆的半径为√(5 - 3) = √2，所以球面与侧面BCC₁B₁的交线为EF，又∠BOE = ∠COF = π/4，所以∠EOF = π/2，所以EF = π/2×√2 = √2π/2。

25. [2023 全国甲卷文,18]如图，在三棱柱 $ ABC - A_1B_1C_1 $ 中，$ A_1C\perp $ 平面 $ ABC $，$ \angle ACB = 90° $.
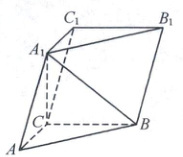
（1）求证：平面 $ ACC_1A_1\perp $ 平面 $ BB_1C_1C $；
（2）设 $ AB = A_1B $，$ AA_1 = 2 $，求四棱锥 $ A_1 - BB_1C_1C $ 的高.

答案：
25.
(1)证明：因为A₁C⊥平面ABC，BC⊂平面ABC，所以A₁C⊥BC；又因为∠ACB = 90°，即AC⊥BC，A₁C，AC⊂平面ACC₁A₁，A₁C∩AC = C，所以BC⊥平面ACC₁A₁。又因为BC⊂平面BB₁C₁C，所以平面ACC₁A₁⊥平面BB₁C₁C。
(2)解：如图，过点A₁作AO⊥CC₁，垂足为O。因为平面ACC₁A₁⊥平面BB₁C₁C，平面ACC₁A₁∩平面BB₁C₁C = CC₁，A₁O⊂平面ACC₁A₁，所以AO⊥平面BB₁C₁C，所以四棱锥A₁ - BB₁C₁C的高为AO。因为A₁C⊥BC，AC⊥BC，A₁B = AB，BC为公共边，所以△A₁BC≌△ABC，所以A₁C = AC；设A₁C = AC = x，则A₁C = x，所以O为CC₁的中点，OC = 1/2AA₁ = 1。又因为A₁C⊥AC，所以AC² + A₁C² = AA₁²，即x² + x² = 2²，解得x = √2。所以AO = √(AC² - OC²) = √[(√2)² - 1²] = 1，所以四棱锥A₁ - BB₁C₁C的高为1。