《2025年小题狂做高中数学必修第二册人教版巅峰版》

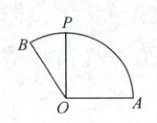
1. [2024 广东梅州期末]如图，在扇形 AOB 中，扇形的半径为 1，∠AOB = $\frac{2π}{3}$，点 P 在弧$\overset{\frown}{AB}$上移动，$\overrightarrow{OP} = a\overrightarrow{OA} + b\overrightarrow{OB}$。当∠AOP = $\frac{π}{2}$时，$a + b$ = (B)


A.$\frac{3}{2}$
B.$\sqrt{3}$
C.2
D.$\frac{3\sqrt{3}}{2}$

答案：
1.B如图，A(1,0)，P(0,1)，又扇形的半径为1，∠AOB=$\frac{2π}{3}$，所以B(cos$\frac{2π}{3}$,sin$\frac{2π}{3}$)，即B(−$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)，所以$\overrightarrow{OA}$=(1,0)，$\overrightarrow{OP}$=(0,1)，$\overrightarrow{OB}$=(−$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).由$\overrightarrow{OP}$=a$\overrightarrow{OA}$+b$\overrightarrow{OB}$，得(0,1)=(a−$\frac{1}{2}$b,$\frac{\sqrt{3}}{2}$b)，即$\begin{cases}a-\frac{1}{2}b=0,\frac{\sqrt{3}}{2}b=1,\end{cases}$解得$\begin{cases}a=\frac{\sqrt{3}}{3},\\b=\frac{2\sqrt{3}}{3}.\end{cases}$所以a+b=$\frac{\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$=$\sqrt{3}$.

2. [2025 江苏宿迁联考]如图，在△ABC 中，D 是 BC 的中点，点 E 在边 AB 上，BE = 2EA，若$\overrightarrow{AB} · \overrightarrow{AC} = 3\overrightarrow{AD} · \overrightarrow{EC}$，则$\frac{AB}{AC}$的值是(A)


A.$\sqrt{3}$
B.2
C.$\sqrt{5}$
D.3

答案： 2.A因为D是BC的中点，所以$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)，又因为点E在边AB上，BE=2EA，$\overrightarrow{EC}$=$\overrightarrow{AC}$−$\overrightarrow{AE}$=$\overrightarrow{AC}$ -$\frac{1}{3}$$\overrightarrow{AB}$，由于$\overrightarrow{AB}$·$\overrightarrow{AC}$=3$\overrightarrow{AD}$·$\overrightarrow{EC}$，所以$\overrightarrow{AB}$·$\overrightarrow{AC}$=3×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)·($\overrightarrow{AC}$−$\frac{1}{3}$$\overrightarrow{AB}$)=$\frac{3}{2}$(−$\frac{1}{3}$$\overrightarrow{AB}$²+$\overrightarrow{AC}$²+$\frac{2}{3}$$\overrightarrow{AB}$·$\overrightarrow{AC}$)=−$\frac{1}{2}$$\overrightarrow{AB}$²+$\frac{3}{2}$$\overrightarrow{AC}$²+$\overrightarrow{AB}$·$\overrightarrow{AC}$，所以$\overrightarrow{AB}$²=3$\overrightarrow{AC}$²，所以$\frac{AB}{AC}$=$\sqrt{3}$

3. [2025 重庆期末]已知△ABC 的外接圆的圆心为 O，且 2$\overrightarrow{AO} = \overrightarrow{AB} + \overrightarrow{AC}$，$|\overrightarrow{OA}| = |\overrightarrow{AC}| = 2$，D 是线段 BC 上一动点，则$\overrightarrow{DA} · \overrightarrow{DB}$的最小值是(C)

A.$-\frac{1}{4}$
B.$-\frac{9}{16}$
C.$-\frac{9}{4}$
D.$-\frac{3}{4}$

答案：
3.C根据2$\overrightarrow{AO}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$，可得$\overrightarrow{AO}$−$\overrightarrow{AB}$=$\overrightarrow{AC}$−$\overrightarrow{AO}$，即$\overrightarrow{BO}$=$\overrightarrow{OC}$，所以AO为边BC上的中线，结合O为△ABC的外心，可得∠BAC=90°.因为|$\overrightarrow{OA}$|=|$\overrightarrow{AC}$|=2，所以|$\overrightarrow{BC}$|=2|$\overrightarrow{OA}$|=4，|$\overrightarrow{AB}$|=$\sqrt{4²−2²}$=2$\sqrt{3}$，由cosB=$\frac{AB}{BC}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$，可得B=30°.设$\overrightarrow{BD}$=λ$\overrightarrow{BC}$(0≤λ≤1)，则$\overrightarrow{DA}$·$\overrightarrow{DB}$=$\overrightarrow{AD}$·$\overrightarrow{BD}$=($\overrightarrow{BD}$−$\overrightarrow{BA}$)·$\overrightarrow{BD}$=|$\overrightarrow{BD}$|²−$\overrightarrow{BA}$·$\overrightarrow{BD}$=λ²|$\overrightarrow{BC}$|²−|$\overrightarrow{BA}$|·|λ$\overrightarrow{BC}$|cos30°=16λ²−2$\sqrt{3}$·4λ·$\frac{\sqrt{3}}{2}$=16λ²−12λ=16(λ−$\frac{3}{8}$)²−$\frac{9}{4}$，所以当λ=$\frac{3}{8}$时，$\overrightarrow{DA}$·$\overrightarrow{DB}$取得最小值−$\frac{9}{4}$.

4. [2023 广东韶关期末]在 Rt△ABC 中，∠BAC = 90°，$|\overrightarrow{AB}| = \frac{1}{t}$，$|\overrightarrow{AC}| = t$，若 P 是△ABC 所在平面内一点，且$\overrightarrow{AP} = \frac{\overrightarrow{AB}}{2|\overrightarrow{AB}|} + \frac{\overrightarrow{AC}}{4|\overrightarrow{AC}|}$，则当$\overrightarrow{PB} · \overrightarrow{PC}$取到最大值时，$t$ = (B)

A.1
B.$\sqrt{2}$
C.$\sqrt{3}$
D.2

答案：
4.B如图，以A为原点，AB，AC所在直线分别为x轴、y轴建立平面直角坐标系.由于|$\overrightarrow{AB}$|=$\frac{1}{t}$，|$\overrightarrow{AC}$|=t，t＞0，则A(0,0)，B($\frac{1}{t}$,0)，C(0,t)，$\overrightarrow{AB}$=($\frac{1}{t}$,0)，$\overrightarrow{AC}$=(0,t).而$\overrightarrow{AP}$=$\frac{\overrightarrow{AB}}{2|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{4|\overrightarrow{AC}|}$=$\frac{t}{2}$($\frac{1}{t}$,0)+$\frac{1}{4t}$(0,t)=($\frac{1}{2}$,$\frac{1}{4}$)，即点P($\frac{1}{2}$,$\frac{1}{4}$)，故$\overrightarrow{PB}$·$\overrightarrow{PC}$=($\frac{1}{t}$−$\frac{1}{2}$,−$\frac{1}{4}$)·(−$\frac{1}{2}$,t−$\frac{1}{4}$)=−$\frac{1}{2t}$+$\frac{t}{4}$+$\frac{5}{16}$.因为t＞0，$\frac{1}{2t}$+$\frac{t}{4}$≥2$\sqrt{\frac{1}{2t}×\frac{t}{4}}$=$\frac{\sqrt{2}}{2}$，当且仅当$\frac{1}{2t}$=$\frac{t}{4}$，即t=$\sqrt{2}$时取等号.故当t=$\sqrt{2}$时，$\overrightarrow{PB}$·$\overrightarrow{PC}$=−$\frac{1}{2t}$+$\frac{t}{4}$+$\frac{5}{16}$取到最大值−$\frac{\sqrt{2}}{2}$+$\frac{5}{16}$.

5. [2025 江苏南京期末]已知菱形 ABCD 的边长为 1，BD = $\sqrt{3}$，M 是菱形 ABCD 所在平面内的动点，则$\overrightarrow{MA} · (\overrightarrow{MB} + \overrightarrow{MC})$的取值范围是(A)

A.$\left[-\frac{3}{8}, +\infty\right)$
B.$\left[-\frac{5}{16}, +\infty\right)$
C.$\left[-\frac{1}{8}, +\infty\right)$
D.$\left[-\frac{3}{16}, +\infty\right)$

答案：
5.A如图，以AC所在直线为x轴，BD所在直线为y轴，建立平面直角坐标系.因为菱形ABCD的边长为1，BD=$\sqrt{3}$，所以A(−$\frac{1}{2}$,0)，B(0,−$\frac{\sqrt{3}}{2}$)，C($\frac{1}{2}$,0)，设M(x,y)，则$\overrightarrow{MA}$=(−$\frac{1}{2}$−x,−y)，$\overrightarrow{MB}$=(−x,−$\frac{\sqrt{3}}{2}$−y)，$\overrightarrow{MC}$=($\frac{1}{2}$−x,−y)，所以$\overrightarrow{MA}$·($\overrightarrow{MB}$ +$\overrightarrow{MC}$)=$\overrightarrow{MA}$·$\overrightarrow{MB}$+$\overrightarrow{MA}$·$\overrightarrow{MC}$=x($\frac{1}{2}$+x)+y($\frac{\sqrt{3}}{2}$+y)+(x+$\frac{1}{2}$)(x−$\frac{1}{2}$)+y²=2x²+$\frac{1}{2}$x+2y²+$\frac{\sqrt{3}}{2}$y−$\frac{1}{4}$=2(x+$\frac{1}{8}$)²+2(y−$\frac{\sqrt{3}}{8}$)²−$\frac{3}{8}$≥−$\frac{3}{8}$，当且仅当x=−$\frac{1}{8}$，y=$\frac{\sqrt{3}}{8}$时，等号成立，所以$\overrightarrow{MA}$·($\overrightarrow{MB}$+$\overrightarrow{MC}$)的取值范围是[−$\frac{3}{8}$,+∞).