《2025年小题狂做高中数学必修第二册人教版巅峰版》

1. [2025 四川成都名校联盟期末]据《九章算术》记载,我国匠人常需计算不同几何体表面积或体积的比例以优化用料,例如,制作圆锥形与球形装饰物时,需比较两者的表面积以确定所需涂漆或覆盖材料的用量.若圆锥的底面直径和母线都等于球的直径,则圆锥与球的表面积之比为 (C)

A.$\frac{2}{3}$
B.$\frac{2}{π}$
C.$\frac{3}{4}$
D.$\frac{4}{π}$

答案： 1.C设球的半径为$r$，则根据题意可得，圆锥与球的表面积之比为$\frac{\pi r^2 + \pi r × 2r}{4 \pi r^2} = \frac{3}{4}$。

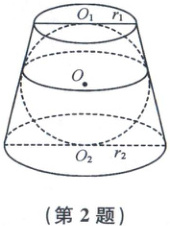
2. [2023 湖北咸宁期末]已知球 O 内切于圆台(即球与该圆台的上、下底面以及侧面均相切),且圆台的上、下底面半径 $r_{1}:r_{2}=2:3$,则圆台的体积与球的体积之比为 (B)

A.$\frac{3}{2}$
B.$\frac{19}{12}$
C.2
D.$\frac{19}{6}$

答案：
2.B如图为该几何体的轴截面，其中圆$O$是等腰梯形$ABCD$的内切圆，设圆$O$与梯形的腰相切于点$E$，与上、下底分别切于点$O_1,O_2$。设球的半径为$r$，圆台上、下底面的半径为$r_1 = 2a,r_2 = 3a$。注意到$OD$与$OA$均为角平分线，因此$\angle DOA = 90°$，从而$\triangle AO_2O \sim \triangle O_1OD$，故$r^2 = r_1r_2 = 6a^2$。设圆台的体积为$V_1$，球的体积为$V_2$，则$\frac{V_1}{V_2} = \frac{\frac{1}{3} × 2r × (\pi r_1^2 + \pi r_2^2 + \pi r_1r_2)}{\frac{4}{3} \pi r^3} = \frac{4a^2 + 9a^2 + 6a^2}{4a^2} = \frac{19}{12}$。
　　 　　

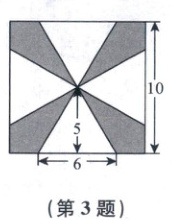
3. [2024 江苏南京一中期末]如图,一块边长为 10 的正方形铁片上有四块阴影部分,将这些阴影部分裁下去,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,则这个正四棱锥的内切球(球与正四棱锥各面均有且只有一个公共点)的体积为 (B)

A.$\frac{9π}{4}$
B.$\frac{9π}{2}$
C.$9π$
D.$\frac{32π}{3}$

答案： 3.B　如图，作出四棱锥$P - ABCD$，根据题意可得正四棱锥的斜高$PM = 5$，底面正方形$ABCD$的边长为$6$，所以正四棱锥的高$OP = \sqrt{5^2 - 3^2} = 4$，设这个正四棱锥的内切球的球心为$Q$，半径为$r$，与侧面相切于点$N$，设高线与斜高的夹角为$\theta$，则$\sin \theta = \frac{OM}{PM} = \frac{3}{5}$，则$OP = OQ + \frac{QN}{\sin \theta}$，即$4 = r + \frac{r}{\sin \theta} = \frac{8}{3}r$，所以$r = \frac{3}{2}$，所以这个正四棱锥的内切球的体积为$\frac{4}{3} \pi r^3 = \frac{4}{3} × \pi × \left( \frac{3}{2} \right)^3 = \frac{9\pi}{2}$。

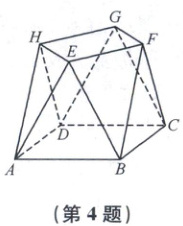
4. [2025 天津期末]如图,空间几何体 $ABCD - EFGH$ 为“四角反棱台”,它是由两个相互平行的正方形经过旋转,连接而成,且上底面正方形的四个顶点在下底面的射影为下底面正方形各边的中点.若 $BE = \sqrt{5},AB = 2$,且所有顶点在同一个球面上,则这个球的表面积为 (B)

A.$12π$
B.$\frac{41π}{4}$
C.$\frac{153π}{16}$
D.$\frac{41π}{8}$

答案：
4.B设球心为$O$，底面正方形$ABCD$的中心为$O_1$，上底面正方形$EFGH$的中心为$O_2$，几何体上、下底面平行且所有顶点在同一球面上，所以球心在直线$O_1O_2$上。已知$AB = 2$，则底面正方形$ABCD$对角线长为$2\sqrt{2}$，所以$O_1B = \sqrt{2}$。上底面正方形$EFGH$边长为$\sqrt{2}$，其对角线为$2$，则$O_2E = 1$。设$OO_1 = h$，则$OO_2 = |OO_1 - h|$，又$BE = \sqrt{5}$，根据勾股定理，在$Rt \triangle OO_1B$，$Rt \triangle OO_2E$中，$R^2 = h^2 + (\sqrt{2})^2$（$R$为球的半径），$R^2 = (OO_1 - h)^2 + 1^2$，过点$F$作$FQ \perp BC$，垂足为$Q$，由题意可知，$Q$为$BC$的中点，在$Rt \triangle FQB$中，$BF = \sqrt{5}$，$BQ = 1$，根据勾股定理可得$FQ = \sqrt{BF^2 - BQ^2} = 2$，即$OO_1 = FQ = 2$，联立可得$h^2 + 2 = (2 - h)^2 + 1$，解得$h = \frac{3}{4}$，代入可得$R^2 = \left( \frac{3}{4} \right)^2 + 2 = \frac{41}{16}$，解得$R = \frac{\sqrt{41}}{4}$，所以球的表面积$S_{球} = 4 \pi R^2 = 4 \pi × \frac{41}{16} = \frac{41\pi}{4}$。
　　　　　

5. [多选题,2025 湖北武汉期末]已知棱长为 a 的正四面体(棱长都相等的三棱锥)的高为 $h = \frac{\sqrt{6}}{3}a$,外接球的半径为 $R = \frac{\sqrt{6}}{4}a$,内切球的半径为 $r = \frac{\sqrt{6}}{12}a$,现有棱长为 a 的正四面体 $A - BCD$ 的内切球的表面积为 $4π$,且表面密封,则下列说法正确的是 (BC)

A.侧棱 $AB$ 与平面 $BCD$ 所成的角的正切值为 $\frac{\sqrt{6}}{3}$
B.正四面体 $A - BCD$ 的外接球的体积为 $36π$
C.若有一个小正四面体 $E - FGH$ 在正四面体 $A - BCD$ 的内部,且可以任意旋转,则小正四面体 $E - FGH$ 的棱长 b 的最大值为 $\frac{1}{3}a$
D.若有一个小正方体在正四面体 $A - BCD$ 的内部,且可以任意旋转,则小正方体的棱长 c 的最大值为 $\frac{\sqrt{2}}{12}a$

答案：
5.BC　如图所示，设点$A$在平面$BCD$内的射影为点$E$，则$AE \perp$平面$BCD$，$\angle ABE$即为侧棱$AB$与平面$BCD$所成的角，因为$BE \subset$平面$BCD$，所以$AE \perp BE$，由题意知$AB = a$，$AE = h = \frac{\sqrt{6}}{3}a$，$BE = \sqrt{AB^2 - AE^2} = \sqrt{a^2 - \left( \frac{\sqrt{6}}{3}a \right)^2} = \frac{\sqrt{3}}{3}a$，所以在$Rt \triangle ABE$中，$\tan \angle ABE = \frac{AE}{BE} = \sqrt{2}$，$\sin \angle ABE = \frac{AE}{AB} = \frac{\sqrt{6}}{3}$，所以侧棱$AB$与平面$BCD$所成的角的正切值为$\sqrt{2}$，正弦值为$\frac{\sqrt{6}}{3}$，故A错误；因为棱长为$a$的正四面体$A - BCD$的内切球的表面积为$4\pi$，所以由$4 \pi r^2 = 4 \pi$，解得$r = 1$，即正四面体$A - BCD$的内切球的半径$r = 1$，则正四面体$A - BCD$的外接球的半径$R = 3r = 3$，体积为$V = \frac{4}{3} \pi R^3 = 36 \pi$，故B正确；当小正四面体$E - FGH$的外接球为正四面体$A - BCD$的内切球时，小正四面体$E - FGH$的棱长$b$取得最大值，此时$\frac{\sqrt{6}}{4} b = \frac{\sqrt{6}}{12} a$，即$b = \frac{1}{3} a$，故C正确；当小正方体$E - FGH$的外接球为正四面体$A - BCD$的内切球时，小正方体的棱长$c$取得最大值，此时$\frac{\sqrt{3}}{2} c = \frac{\sqrt{6}}{12} a$，即$c = \frac{\sqrt{2}}{6} a$，故D错误。