《2025年小题狂做高中数学必修第二册人教版巅峰版》

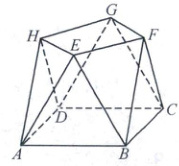
28. [2022 全国甲卷文,19]小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示，底面 $ ABCD $ 是边长为 8（单位：cm）的正方形，$ \triangle EAB,\triangle FBC,\triangle GCD,\triangle HDA $ 均为正三角形，且它们所在的平面都与平面 $ ABCD $ 垂直.
（1）求证：$ EF// $ 平面 $ ABCD $；
（2）求该包装盒的容积（不计包装盒材料的厚度）.

答案：
28.
(1)证明：如图所示，分别取AB，BC的中点M，N，连接EM，FN，MN。因为△EAB，△FBC为全等的正三角形，所以EM⊥AB，FN⊥BC，EM = FN。又平面EAB⊥平面ABCD，平面EAB∩平面ABCD = AB，EM⊂平面EAB，所以EM⊥平面ABCD。同理可得FN⊥平面ABCD。根据线面垂直的性质定理可知EM//FN，又EM = FN，所以四边形EMNF为平行四边形，所以EF//MN，又EF⊄平面ABCD，MN⊂平面ABCD，所以EF//平面ABCD。

(2)解：如图所示，分别取AD，DC中点K，L，连接HK，KM，GL，LN，KL。由
(1)知，EF//MN且EF = MN，同理，HE//KM，HE = KM，HG//KL，HG = KL，GF//LN，GF = LN。由平面知识可知，BD⊥MN，MN⊥MK，KM = MN = NL = LK，所以该几何体的体积等于长方体KMNL - HEFG的体积加上四棱锥B - MNFE体积的4倍。因为MN = NL = LK = KM = 4√2，EM = 8sin60° = 4√3，点B到平面MNFE的距离即为点B到直线MN的距离d，d = 2√2，所以该几何体的体积V = (4√2)²×4√3 + 4×(1/3)×4√2×4√3×2√2 = 128√3 + 256√3/3 = 640√3/3。

29. [2024 新高考Ⅰ卷,17]如图，在四棱锥 $ P - ABCD $ 中，$ PA\perp $ 底面 $ ABCD $，$ PA = AC = 2 $，$ BC = 1 $，$ AB = \sqrt{3} $.
（1）若 $ AD\perp PB $，求证：$ AD// $ 平面 $ PBC $；
（2）若 $ AD\perp DC $，且二面角 $ A - CP - D $ 的正弦值为 $ \frac{\sqrt{42}}{7} $，求 $ AD $.

答案：
29.
(1)证明：因为PA⊥平面ABCD，AD⊂平面ABCD，所以PA⊥AD。又因为AD⊥PB，PA∩PB = P，PA，PB⊂平面PAB，所以AD⊥平面PAB。因为AB⊂平面PAB，所以AD⊥AB。在△ABC中，AB² + BC² = AC²，所以AB⊥BC。因为A，B，C，D四点共面，所以AD//BC。又因为BC⊂平面PBC，AD⊄平面PBC，所以AD//平面PBC。
(2)解：过点D作DO⊥AC，垂足为O。因为PA⊥底面ABCD，PA⊂平面PAC，所以平面PAC⊥平面ABCD。又平面PAC∩平面ABCD = AC，DO⊂平面ABCD，所以DO⊥平面PAC。因为PC⊂平面PAC，所以DO⊥PC；再过点O作OG⊥PC，垂足为G，连接DG。因为DO∩OG = O，DO，OG⊂平面DOG，所以PC⊥平面DOG。又DG⊂平面DOG，所以PC⊥DG，所以∠DGO为二面角A - CP - D的平面角。因为DO⊥平面PAC，OG⊂平面PAC，所以DO⊥OG，在Rt△DOG中，sin∠DGO = DO/DG ①。在Rt△ADC中，AC = 2，设AD = x，则DC = √(4 - x²)，所以1/2AD·DC = 1/2AC·DO，所以DO = (AD·DC)/AC = x√(4 - x²)/2 ②。因为PA⊥底面ABCD，DC⊂平面ABCD，所以PA⊥CD。又AD⊥CD，PA∩AD = A，PA，AD⊂平面PAD，所以CD⊥平面PAD。又PD⊂平面PAD，所以CD⊥PD。因为PA⊥底面ABCD，AD，AC⊂平面ABCD，所以PA⊥AD，PA⊥AC；在Rt△PAD中，PD = √(PA² + AD²) = √(4 + x²)；在Rt△PAC中，PC = √(PA² + AC²) = 2√2。在Rt△PDC中，1/2PD·DC = 1/2PC·DG，所以DG = (PD·DC)/PC = [√(4 + x²)×√(4 - x²)]/(2√2) ③。将②式和③式代入①式，得√42/7 = [x√(4 - x²)/2]/[√(4 + x²)×√(4 - x²)/(2√2)]，即√6/√7 = x/√(4 + x²)，解得x = √3，所以AD = √3。