2025年小题狂做高中数学必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. [2024江苏盐城中学期中]已知在△ABC中,角A,B,C的对边分别为a,b,c,若B= $\frac{\pi}{6}$,b= $\sqrt{2}$,c=2,则C= (
A.$\frac{\pi}{4}$
B.$\frac{\pi}{4}$或$\frac{3\pi}{4}$
C.$\frac{3\pi}{4}$
D.$\frac{\pi}{3}$或$\frac{2\pi}{3}$
B
)A.$\frac{\pi}{4}$
B.$\frac{\pi}{4}$或$\frac{3\pi}{4}$
C.$\frac{3\pi}{4}$
D.$\frac{\pi}{3}$或$\frac{2\pi}{3}$
答案:
1.B 由正弦定理得$\frac{b}{\sin B}=\frac{c}{\sin C}$,所以$\sin C=\frac{c\sin B}{b}=\frac{2×\sin\frac{\pi}{6}}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.因为$c>b$,所以$C>B$,所以$C=\frac{\pi}{4}$或$\frac{3\pi}{4}$.
2. [2025江苏太湖中学月考]已知△ABC的内角A,B,C所对的边分别为a,b,c,若tan B=2tan C,b=2,则△ABC面积的最大值为 (
A.$\frac{3}{4}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{2}$
D.$\frac{3}{2}$
D
)A.$\frac{3}{4}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{2}$
D.$\frac{3}{2}$
答案:
2.D 因为$\tan B = 2\tan C$,所以$\frac{\sin B}{\cos B}=\frac{2\sin C}{\cos C}$,即$\sin B\cos C = 2\cos B\sin C$,所以$\sin B\cos C+\cos B\sin C=3\cos B\sin C$,所以$\sin(B + C)=3\cos B\sin C=\sin A$,由正弦定理知$a = 3c\cos B$,即$\cos B=\frac{a}{3c}$,所以$\sin B=\sqrt{1-\frac{a^{2}}{9c^{2}}}$,由余弦定理知$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{a}{3c}$,化简得$3c^{2}=3b^{2}-a^{2}=12 - a^{2}$,所以$\triangle ABC$的面积$S=\frac{1}{2}ac\sin B=\frac{1}{2}ac\sqrt{1-\frac{a^{2}}{9c^{2}}}=\frac{1}{2}\sqrt{\frac{3a^{2}·3c^{2}-a^{4}}{9}}=\frac{1}{2}\sqrt{\frac{3a^{2}(12 - a^{2})-a^{4}}{9}}=\frac{1}{3}\sqrt{-a^{4}+9a^{2}}=\frac{1}{3}\sqrt{-(a^{2}-\frac{9}{2})^{2}+\frac{81}{4}}$,当$a^{2}=\frac{9}{2}$时,$S$有最大值$\frac{3}{2}$.
3. [2025河北文安一中期末]在△ABC中,内角A,B,C的对边分别为a,b,c,已知b=2a cos $(C - \frac{\pi}{3})$,则$\frac{\sin 2A}{1 + \cos 2A}$ = (
A.$\frac{\sqrt{2}}{3}$
B.$\sqrt{2}$
C.$\sqrt{3}$
D.$\frac{\sqrt{3}}{3}$
D
)A.$\frac{\sqrt{2}}{3}$
B.$\sqrt{2}$
C.$\sqrt{3}$
D.$\frac{\sqrt{3}}{3}$
答案:
3.D 因为$b = 2a\cos(C - \frac{\pi}{3})$,所以由正弦定理可得$\sin B = 2\sin A\cos(C - \frac{\pi}{3}) = 2\sin A(\cos C\cos\frac{\pi}{3}+\sin C\sin\frac{\pi}{3})=\sin A\cos C+\sqrt{3}\sin A\sin C$,而$\sin B=\sin(A + C)=\sin A\cos C+\cos A\sin C$,故$\cos A\sin C=\sqrt{3}\sin A\sin C$,由于在$\triangle ABC$中,$\sin C\neq0$,可得$\tan A=\frac{\sqrt{3}}{3}$.在$\triangle ABC$中,$A\in(0,\pi)$,可得$A=\frac{\pi}{6}$,故$\frac{\sin2A}{1 + \cos2A}=\frac{\frac{\sqrt{3}}{2}}{1+\frac{1}{2}}=\frac{\sqrt{3}}{3}$.
4. [多选题,2024福建厦门中学期末]如图,正方形ABCD的边长为1,P,Q分别为线段AB,AD上的动点,则下列说法正确的是 (
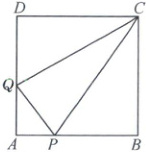
A.当P,Q分别为线段AB,CD的中点时,cos∠PCQ= $\frac{4}{5}$
B.当AP+AQ=1时,tan∠PCQ的最小值为$\frac{3}{4}$
C.当△APQ的周长为2时,∠PCQ= $\frac{\pi}{3}$
D.当∠BCP+∠DCQ= $\frac{\pi}{3}$时,$\overrightarrow{CP} · \overrightarrow{CQ}$的取值范围是$[\frac{2\sqrt{3}}{3},\sqrt{3})$
AB
)
A.当P,Q分别为线段AB,CD的中点时,cos∠PCQ= $\frac{4}{5}$
B.当AP+AQ=1时,tan∠PCQ的最小值为$\frac{3}{4}$
C.当△APQ的周长为2时,∠PCQ= $\frac{\pi}{3}$
D.当∠BCP+∠DCQ= $\frac{\pi}{3}$时,$\overrightarrow{CP} · \overrightarrow{CQ}$的取值范围是$[\frac{2\sqrt{3}}{3},\sqrt{3})$
答案:
4.AB 对于A,当$P,Q$分别为线段$AB,CD$的中点时,$PC = QC=\sqrt{1^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{5}}{2},PQ=\frac{\sqrt{2}}{2}$,在$\triangle PCQ$中,由余弦定理得$\cos\angle PCQ=\frac{PC^{2}+QC^{2}-PQ^{2}}{2PC× QC}=\frac{\frac{5}{4}+\frac{5}{4}-\frac{1}{2}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{5}}{2}}=\frac{4}{5}$,故A正确;对于B,当$AP + AQ = 1$时,设$AP = t$,所以$AQ = 1 - t$,$t\in[0,1]$,连接$AC$,则$\tan\angle DCQ=\frac{DQ}{DC}=t,\tan\angle BCP=\frac{PB}{BC}=1 - t$, $\tan\angle PCQ=\tan(\frac{\pi}{2}-\angle DCQ - \angle BCP)=\frac{1}{\tan(\angle DCQ+\angle BCP)}=\frac{1 - \tan\angle DCQ\tan\angle BCP}{\tan\angle DCQ+\tan\angle BCP}=1 - t(1 - t)=(t - \frac{1}{2})^{2}+\frac{3}{4}$,故$\tan\angle PCQ$的最小值为$\frac{3}{4}$,故B正确;对于C,当$\triangle APQ$的周长为$2$时,由于$\triangle APQ$为直角三角形,不妨取$AP = AQ = 2 - \sqrt{2}$,则$PQ=\sqrt{2}(2 - \sqrt{2})=2(\sqrt{2}-1)$,则$PB = DQ=\sqrt{2}-1$,所以$PC = QC=\sqrt{1+(\sqrt{2}-1)^{2}}=\sqrt{4 - 2\sqrt{2}}$,此时$PC = QC\neq PQ$,则$\angle PCQ\neq\frac{\pi}{3}$,否则$\triangle APQ$为正三角形,与$PC = QC\neq PQ$矛盾,故C错误;对于D,当$\angle BCP+\angle DCQ=\frac{\pi}{3}$时,$\angle PCQ=\frac{\pi}{6}$,设$\angle BCP=\alpha$,且$\alpha\leq\frac{\pi}{4},\frac{\pi}{3}-\alpha\leq\frac{\pi}{4}$,即$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,则$CP=\frac{1}{\cos\alpha},CQ=\frac{1}{\cos(\frac{\pi}{3}-\alpha)}$,故$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{1}{\cos\alpha}×\frac{1}{\cos(\frac{\pi}{3}-\alpha)}×\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2\cos\alpha\cos(\frac{\pi}{3}-\alpha)}$而$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\cos^{2}\alpha+\sqrt{3}\cos\alpha\sin\alpha=\frac{\sqrt{3}}{2}\sin2\alpha+\frac{1}{2}\cos2\alpha+\frac{1}{2}=\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}$,而$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,所以$2\alpha+\frac{\pi}{6}\in[\frac{\pi}{3},\frac{2\pi}{3}]$,故$\sin(2\alpha+\frac{\pi}{6})\in[\frac{\sqrt{3}}{2},1]$,则$\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}\in[\frac{\sqrt{3}+1}{2},\frac{3}{2}]$,即当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{\sqrt{3}+1}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{\sqrt{3}+1}{2}}=\sqrt{3}(\sqrt{3}-1)$,当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{3}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{3}{2}}=\frac{2\sqrt{3}}{3}$,故$\overrightarrow{CP}·\overrightarrow{CQ}\in[\frac{2\sqrt{3}}{3},3 - \sqrt{3}]$,故D错误.
$\tan\angle PCQ=\tan(\frac{\pi}{2}-\angle DCQ - \angle BCP)=\frac{1}{\tan(\angle DCQ+\angle BCP)}=\frac{1 - \tan\angle DCQ\tan\angle BCP}{\tan\angle DCQ+\tan\angle BCP}=1 - t(1 - t)=(t - \frac{1}{2})^{2}+\frac{3}{4}$,故$\tan\angle PCQ$的最小值为$\frac{3}{4}$,故B正确;对于C,当$\triangle APQ$的周长为$2$时,由于$\triangle APQ$为直角三角形,不妨取$AP = AQ = 2 - \sqrt{2}$,则$PQ=\sqrt{2}(2 - \sqrt{2})=2(\sqrt{2}-1)$,则$PB = DQ=\sqrt{2}-1$,所以$PC = QC=\sqrt{1+(\sqrt{2}-1)^{2}}=\sqrt{4 - 2\sqrt{2}}$,此时$PC = QC\neq PQ$,则$\angle PCQ\neq\frac{\pi}{3}$,否则$\triangle APQ$为正三角形,与$PC = QC\neq PQ$矛盾,故C错误;对于D,当$\angle BCP+\angle DCQ=\frac{\pi}{3}$时,$\angle PCQ=\frac{\pi}{6}$,设$\angle BCP=\alpha$,且$\alpha\leq\frac{\pi}{4},\frac{\pi}{3}-\alpha\leq\frac{\pi}{4}$,即$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,则$CP=\frac{1}{\cos\alpha},CQ=\frac{1}{\cos(\frac{\pi}{3}-\alpha)}$,故$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{1}{\cos\alpha}×\frac{1}{\cos(\frac{\pi}{3}-\alpha)}×\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2\cos\alpha\cos(\frac{\pi}{3}-\alpha)}$而$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\cos^{2}\alpha+\sqrt{3}\cos\alpha\sin\alpha=\frac{\sqrt{3}}{2}\sin2\alpha+\frac{1}{2}\cos2\alpha+\frac{1}{2}=\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}$,而$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,所以$2\alpha+\frac{\pi}{6}\in[\frac{\pi}{3},\frac{2\pi}{3}]$,故$\sin(2\alpha+\frac{\pi}{6})\in[\frac{\sqrt{3}}{2},1]$,则$\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}\in[\frac{\sqrt{3}+1}{2},\frac{3}{2}]$,即当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{\sqrt{3}+1}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{\sqrt{3}+1}{2}}=\sqrt{3}(\sqrt{3}-1)$,当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{3}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{3}{2}}=\frac{2\sqrt{3}}{3}$,故$\overrightarrow{CP}·\overrightarrow{CQ}\in[\frac{2\sqrt{3}}{3},3 - \sqrt{3}]$,故D错误.
4.AB 对于A,当$P,Q$分别为线段$AB,CD$的中点时,$PC = QC=\sqrt{1^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{5}}{2},PQ=\frac{\sqrt{2}}{2}$,在$\triangle PCQ$中,由余弦定理得$\cos\angle PCQ=\frac{PC^{2}+QC^{2}-PQ^{2}}{2PC× QC}=\frac{\frac{5}{4}+\frac{5}{4}-\frac{1}{2}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{5}}{2}}=\frac{4}{5}$,故A正确;对于B,当$AP + AQ = 1$时,设$AP = t$,所以$AQ = 1 - t$,$t\in[0,1]$,连接$AC$,则$\tan\angle DCQ=\frac{DQ}{DC}=t,\tan\angle BCP=\frac{PB}{BC}=1 - t$,
 $\tan\angle PCQ=\tan(\frac{\pi}{2}-\angle DCQ - \angle BCP)=\frac{1}{\tan(\angle DCQ+\angle BCP)}=\frac{1 - \tan\angle DCQ\tan\angle BCP}{\tan\angle DCQ+\tan\angle BCP}=1 - t(1 - t)=(t - \frac{1}{2})^{2}+\frac{3}{4}$,故$\tan\angle PCQ$的最小值为$\frac{3}{4}$,故B正确;对于C,当$\triangle APQ$的周长为$2$时,由于$\triangle APQ$为直角三角形,不妨取$AP = AQ = 2 - \sqrt{2}$,则$PQ=\sqrt{2}(2 - \sqrt{2})=2(\sqrt{2}-1)$,则$PB = DQ=\sqrt{2}-1$,所以$PC = QC=\sqrt{1+(\sqrt{2}-1)^{2}}=\sqrt{4 - 2\sqrt{2}}$,此时$PC = QC\neq PQ$,则$\angle PCQ\neq\frac{\pi}{3}$,否则$\triangle APQ$为正三角形,与$PC = QC\neq PQ$矛盾,故C错误;对于D,当$\angle BCP+\angle DCQ=\frac{\pi}{3}$时,$\angle PCQ=\frac{\pi}{6}$,设$\angle BCP=\alpha$,且$\alpha\leq\frac{\pi}{4},\frac{\pi}{3}-\alpha\leq\frac{\pi}{4}$,即$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,则$CP=\frac{1}{\cos\alpha},CQ=\frac{1}{\cos(\frac{\pi}{3}-\alpha)}$,故$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{1}{\cos\alpha}×\frac{1}{\cos(\frac{\pi}{3}-\alpha)}×\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2\cos\alpha\cos(\frac{\pi}{3}-\alpha)}$而$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\cos^{2}\alpha+\sqrt{3}\cos\alpha\sin\alpha=\frac{\sqrt{3}}{2}\sin2\alpha+\frac{1}{2}\cos2\alpha+\frac{1}{2}=\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}$,而$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,所以$2\alpha+\frac{\pi}{6}\in[\frac{\pi}{3},\frac{2\pi}{3}]$,故$\sin(2\alpha+\frac{\pi}{6})\in[\frac{\sqrt{3}}{2},1]$,则$\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}\in[\frac{\sqrt{3}+1}{2},\frac{3}{2}]$,即当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{\sqrt{3}+1}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{\sqrt{3}+1}{2}}=\sqrt{3}(\sqrt{3}-1)$,当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{3}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{3}{2}}=\frac{2\sqrt{3}}{3}$,故$\overrightarrow{CP}·\overrightarrow{CQ}\in[\frac{2\sqrt{3}}{3},3 - \sqrt{3}]$,故D错误.
$\tan\angle PCQ=\tan(\frac{\pi}{2}-\angle DCQ - \angle BCP)=\frac{1}{\tan(\angle DCQ+\angle BCP)}=\frac{1 - \tan\angle DCQ\tan\angle BCP}{\tan\angle DCQ+\tan\angle BCP}=1 - t(1 - t)=(t - \frac{1}{2})^{2}+\frac{3}{4}$,故$\tan\angle PCQ$的最小值为$\frac{3}{4}$,故B正确;对于C,当$\triangle APQ$的周长为$2$时,由于$\triangle APQ$为直角三角形,不妨取$AP = AQ = 2 - \sqrt{2}$,则$PQ=\sqrt{2}(2 - \sqrt{2})=2(\sqrt{2}-1)$,则$PB = DQ=\sqrt{2}-1$,所以$PC = QC=\sqrt{1+(\sqrt{2}-1)^{2}}=\sqrt{4 - 2\sqrt{2}}$,此时$PC = QC\neq PQ$,则$\angle PCQ\neq\frac{\pi}{3}$,否则$\triangle APQ$为正三角形,与$PC = QC\neq PQ$矛盾,故C错误;对于D,当$\angle BCP+\angle DCQ=\frac{\pi}{3}$时,$\angle PCQ=\frac{\pi}{6}$,设$\angle BCP=\alpha$,且$\alpha\leq\frac{\pi}{4},\frac{\pi}{3}-\alpha\leq\frac{\pi}{4}$,即$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,则$CP=\frac{1}{\cos\alpha},CQ=\frac{1}{\cos(\frac{\pi}{3}-\alpha)}$,故$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{1}{\cos\alpha}×\frac{1}{\cos(\frac{\pi}{3}-\alpha)}×\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2\cos\alpha\cos(\frac{\pi}{3}-\alpha)}$而$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\cos^{2}\alpha+\sqrt{3}\cos\alpha\sin\alpha=\frac{\sqrt{3}}{2}\sin2\alpha+\frac{1}{2}\cos2\alpha+\frac{1}{2}=\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}$,而$\alpha\in[\frac{\pi}{12},\frac{\pi}{4}]$,所以$2\alpha+\frac{\pi}{6}\in[\frac{\pi}{3},\frac{2\pi}{3}]$,故$\sin(2\alpha+\frac{\pi}{6})\in[\frac{\sqrt{3}}{2},1]$,则$\sin(2\alpha+\frac{\pi}{6})+\frac{1}{2}\in[\frac{\sqrt{3}+1}{2},\frac{3}{2}]$,即当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{\sqrt{3}+1}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{\sqrt{3}+1}{2}}=\sqrt{3}(\sqrt{3}-1)$,当$2\cos\alpha\cos(\frac{\pi}{3}-\alpha)=\frac{3}{2}$时,$\overrightarrow{CP}·\overrightarrow{CQ}=\frac{\sqrt{3}}{\frac{3}{2}}=\frac{2\sqrt{3}}{3}$,故$\overrightarrow{CP}·\overrightarrow{CQ}\in[\frac{2\sqrt{3}}{3},3 - \sqrt{3}]$,故D错误. 5. [2023江苏苏州八校期末联考]已知在△ABC中,$\overrightarrow{AB} · \overrightarrow{AC}$=9,sin B=cos A sin C,$S_{\triangle ABC}$=6,P为线段AB上的动点,且$\overrightarrow{CP}$=x·$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$+y·$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$,则$\frac{2}{x}$+$\frac{1}{y}$的最小值为 (
A.$\frac{11}{6}$+$\frac{\sqrt{6}}{3}$
B.$\frac{11}{6}$
C.$\frac{11}{12}$+$\frac{\sqrt{6}}{3}$
D.$\frac{11}{12}$
C
)A.$\frac{11}{6}$+$\frac{\sqrt{6}}{3}$
B.$\frac{11}{6}$
C.$\frac{11}{12}$+$\frac{\sqrt{6}}{3}$
D.$\frac{11}{12}$
答案:
5.C 设$|\overrightarrow{AB}| = c,|\overrightarrow{AC}| = b$,根据题意得$\begin{cases}bc\cos A = 9,\\b = c\cos A,\frac{1}{2}bc\sin A = 6,\end{cases}$解得$b = 3,c = 5,\sin A=\frac{4}{5},\cos A=\frac{3}{5}$,$|\overrightarrow{CB}|=\sqrt{(\overrightarrow{AB}-\overrightarrow{AC})^{2}}=\sqrt{c^{2}+b^{2}-2bc\cos A}=4$,所以$\overrightarrow{CP}=x·\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}+y·\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}=\frac{x}{3}\overrightarrow{CA}+\frac{y}{4}\overrightarrow{CB}$.又因为$A,P,B$三点共线,所以$\frac{x}{3}+\frac{y}{4}=1$.所以$\frac{2}{x}+\frac{1}{y}=(\frac{x}{3}+\frac{y}{4})(\frac{2}{x}+\frac{1}{y})=\frac{11}{12}+\frac{x}{3y}+\frac{y}{2x}\geq\frac{11}{12}+2\sqrt{\frac{x}{3y}·\frac{y}{2x}}=\frac{11}{12}+\frac{\sqrt{6}}{3}$,当且仅当$\begin{cases}\frac{x}{3y}=\frac{y}{2x},\frac{x}{3}+\frac{y}{4}=1,\end{cases}$即$\begin{cases}x=\frac{6×(4 - \sqrt{6})}{5},\\y=\frac{4×(2\sqrt{6}-3)}{5}\end{cases}$时,等号成立.
6. [生活生产,2025江苏南京五校共同体期末]如图,将一圆形纸片沿直径AB对折,使圆上两点C,C₁重合,D,E为直径AB上两点,且∠ECD=30°,对折后沿直线DC,EC裁剪,展开得到四边形CEC₁D.若该圆形的直径为2,AC= $\frac{1}{2}$AB,则当四边形CEC₁D的面积最小时,DE=
 ]
]
2√3-3
. ]
]
答案:
6.$2\sqrt{3}-3$ 设圆的圆心为$O$,因为圆的直径$AB = 2,AC=\frac{1}{2}AB = 1$,故$\triangle AOC$为等边三角形,$\angle COA = 60^{\circ}$,点$C$到$AB$的距离为$\frac{\sqrt{3}}{2}$,四边形$CEC_{1}D$的面积为$2S_{\triangle CED}=\frac{\sqrt{3}}{2}· DE$,因此求面积的最小值即求$DE$长的最小值.过点$C$作$CH\perp ED$于点$A$,设$EH = x,DH = y,DE = x + y = t$,由$\angle ECD = 30^{\circ}$,利用正切和角公式,得$\frac{\frac{2x}{\sqrt{3}}+\frac{2y}{\sqrt{3}}}{1-\frac{4xy}{3}}=\frac{1}{\sqrt{3}}$,化简得$2t = 1-\frac{4xy}{3}$,即$4xy = 3(1 - 2t)$,结合基本不等式,得$xy\leq(\frac{x + y}{2})^{2}=\frac{t^{2}}{4}$,代入得$t^{2}+6t - 3\geq0$,解得$t\geq - 3 + 2\sqrt{3}$(舍负),当且仅当$x = y$时取等号,因此,$DE$的最小值为$2\sqrt{3}-3$.
7. [2024广东佛山期末]已知在△ABC中,角A,B,C的对边分别是a,b,c,若(2b - c)·cos A - a cos C=0,点D在边BC上,AD是角A的平分线,且AD=3,则△ABC面积的最小值是
3√3
.
答案:
7.$3\sqrt{3}$ 因为$(2b - c)\cos A - a\cos C = 0$,由正弦定理可得$(2\sin B - \sin C)\cos A - \sin A\cos C = 0$,即$2\sin B\cos A - \sin C\cos A - \sin A\cos C = 0$,所以$2\sin B\cos A - \sin(A + C)=0$,即$2\sin B\cos A - \sin B = 0$.因为$B\in(0,\pi)$,所以$\sin B>0$,所以$\cos A=\frac{1}{2}$,而$A\in(0,\pi)$,则$A=\frac{\pi}{3}$.因为$AD$是角$A$的平分线,所以$\angle BAD=\angle CAD=\frac{\pi}{6}$.因为$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$,即$\frac{1}{2}bc\sin\angle BAC=\frac{1}{2}c· AD\sin\angle BAD+\frac{1}{2}b· AD\sin\angle CAD,AD = 3$,可得$bc = \sqrt{3}(b + c)$.因为$b + c\geq2\sqrt{bc}$,当且仅当$b = c$时,等号成立,即$bc\geq2\sqrt{3}\sqrt{bc}$,所以$bc\geq12$,所以$S_{\triangle ABC}=\frac{1}{2}bc\sin A=\frac{\sqrt{3}}{4}bc\geq3\sqrt{3}$,当且仅当$b = c = 2\sqrt{3}$时取等号,所以$\triangle ABC$面积的最小值为$3\sqrt{3}$.
查看更多完整答案,请扫码查看


