2025年天利38套五年真题高考试题分类化学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套五年真题高考试题分类化学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
5.(2022·河北卷,14分)氢能是极具发展潜力的清洁能源,以氢燃料为代表的燃料电池有良好的应用前景。
(1)$298\ K$时,$1\ g\ {H_{2}}$燃烧生成${H_{2}O(g)}$放热$121\ kJ$,$1\ mol\ {H_{2}O(l)}$蒸发吸热$44\ kJ$,表示${H_{2}}$燃烧热的热化学方程式为_______。
(2)工业上常用甲烷水蒸气重整制备氢气,体系中发生如下反应。
Ⅰ.${CH_{4}(g) + H_{2}O(g)⇌ CO(g) + 3H_{2}(g)}$
Ⅱ.${CO(g) + H_{2}O(g)⇌ CO_{2}(g) + H_{2}(g)}$
①下列操作中,能提高${CH_{4}(g)}$平衡转化率的是_______(填标号)。
A.增加${CH_{4}(g)}$用量
B.恒温恒压下通入惰性气体
C.移除${CO(g)}$
D.加入催化剂
②恒温恒压条件下,$1\ mol\ {CH_{4}(g)}$和$1\ mol\ {H_{2}O(g)}$反应达平衡时,${CH_{4}(g)}$的转化率为$\alpha$,${CO_{2}(g)}$的物质的量为$b\ mol$,则反应Ⅰ的平衡常数$K_{x}=$_______[写出含有$\alpha$、$b$的计算式;对于反应$m{A(g)} + n{B(g)⇌ }p{C(g)} + q{D(g)}$,$K_{x}=\dfrac{x^{p}(C)· x^{q}(D)}{x^{m}(A)· x^{n}(B)}$,$x$为物质的量分数]。其他条件不变,${H_{2}O(g)}$起始量增加到$5\ mol$,达平衡时,$\alpha =0.90$,$b=0.65$,平衡体系中${H_{2}(g)}$的物质的量分数为_______(结果保留两位有效数字)。
(3)氢氧燃料电池中氢气在_______(填“正”或“负”)极发生反应。
(4)在允许${O^{2-}}$自由迁移的固体电解质燃料电池中,${C_{n}H_{2n+2}}$放电的电极反应式为_______。
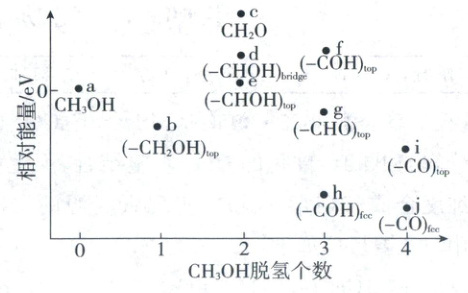
(5)甲醇燃料电池中,吸附在催化剂表面的甲醇分子逐步脱氢得到${CO}$,四步可能脱氢产物及其相对能量如图,则最可行途径为$a\to$_______(用b\simj等代号表示)。
(1)$298\ K$时,$1\ g\ {H_{2}}$燃烧生成${H_{2}O(g)}$放热$121\ kJ$,$1\ mol\ {H_{2}O(l)}$蒸发吸热$44\ kJ$,表示${H_{2}}$燃烧热的热化学方程式为_______。
(2)工业上常用甲烷水蒸气重整制备氢气,体系中发生如下反应。
Ⅰ.${CH_{4}(g) + H_{2}O(g)⇌ CO(g) + 3H_{2}(g)}$
Ⅱ.${CO(g) + H_{2}O(g)⇌ CO_{2}(g) + H_{2}(g)}$
①下列操作中,能提高${CH_{4}(g)}$平衡转化率的是_______(填标号)。
A.增加${CH_{4}(g)}$用量
B.恒温恒压下通入惰性气体
C.移除${CO(g)}$
D.加入催化剂
②恒温恒压条件下,$1\ mol\ {CH_{4}(g)}$和$1\ mol\ {H_{2}O(g)}$反应达平衡时,${CH_{4}(g)}$的转化率为$\alpha$,${CO_{2}(g)}$的物质的量为$b\ mol$,则反应Ⅰ的平衡常数$K_{x}=$_______[写出含有$\alpha$、$b$的计算式;对于反应$m{A(g)} + n{B(g)⇌ }p{C(g)} + q{D(g)}$,$K_{x}=\dfrac{x^{p}(C)· x^{q}(D)}{x^{m}(A)· x^{n}(B)}$,$x$为物质的量分数]。其他条件不变,${H_{2}O(g)}$起始量增加到$5\ mol$,达平衡时,$\alpha =0.90$,$b=0.65$,平衡体系中${H_{2}(g)}$的物质的量分数为_______(结果保留两位有效数字)。
(3)氢氧燃料电池中氢气在_______(填“正”或“负”)极发生反应。
(4)在允许${O^{2-}}$自由迁移的固体电解质燃料电池中,${C_{n}H_{2n+2}}$放电的电极反应式为_______。
(5)甲醇燃料电池中,吸附在催化剂表面的甲醇分子逐步脱氢得到${CO}$,四步可能脱氢产物及其相对能量如图,则最可行途径为$a\to$_______(用b\simj等代号表示)。

答案:
$(1)H_2(g) + \frac{1}{2}O_2(g) \xlongequal{} H_2O(l) \Delta H = -286 kJ/mol $
$(2)①BC ②\frac{(\alpha - b) × (3\alpha + b)^3}{(1 - \alpha) × (1 - \alpha - b) × (2 + 2\alpha)^2} 43\% $
(3)负
$(4)C_nH_{2n + 2} - (6n + 2)e^- + (3n + 1)O^{2-} \xlongequal{} nCO_2 + (n + 1)H_2O $
$(5)b \rightarrow e \rightarrow h \rightarrow j $
【解析】燃烧热、盖斯定律、化学平衡的移动、化学平衡常数的计算、电极反应式书写
(1)根据题目信息写出热化学方程式:
$①H_2(g) + \frac{1}{2}O_2(g) \xlongequal{} H_2O(g) \Delta H_1 = -242 kJ/mol,$
$②H_2O(l) \xlongequal{} H_2O(g) \Delta H_2 = +44 kJ/mol,$$H_2 $燃烧热指$ 1 mol H_2 $完全燃烧生成$H_2O(l) $放出的热量,根据盖斯定律可得出$H_2(g) + \frac{1}{2}O_2(g) \xlongequal{} H_2O(l) \Delta H = \Delta H_1 - \Delta H_2 = -286 kJ/mol。$
(2)①增加甲烷用量会增大$H_2O(g) $的平衡转化率,甲烷平衡转化率减小,A错误;恒温恒压下通入惰性气体,使得体系中各物质浓度减小,其结果等效于减小压强,平衡向气体分子数增加的方向移动,即反应Ⅰ平衡正向移动,甲烷平衡转化率增大,B正确;移除一氧化碳可使反应Ⅰ平衡正向移动,甲烷平衡转化率增大,C正确;加入催化剂可加快反应速率,缩短达到平衡的时间,不会引起平衡移动,甲烷平衡转化率不变,D错误。②两个反应的转化量表示如下:
$Ⅰ CH_4(g) + H_2O(g) \rightleftharpoons CO(g) + 3H_2(g) $
$\Delta n \alpha mol \alpha mol \alpha mol 3\alpha mol $
$Ⅱ CO(g) + H_2O(g) \rightleftharpoons CO_2(g) + H_2(g) $
$\Delta n b mol b mol b mol b mol $
反应Ⅱ气体物质的量不变,气体总物质的量的变化由反应Ⅰ引起,平衡时n(总$) = (2 + 2\alpha) mol,$$n(CH_4) = (1 - \alpha) mol,$$n(H_2O) = (1 - \alpha - b) mol,$$n(CO) = (\alpha - b) mol,$$n(H_2) = (3\alpha + b) mol,$
反应Ⅰ的平衡常数$K_x = \frac{x(CO) × x^3(H_2)}{x(CH_4) × x(H_2O)} = \frac{\frac{\alpha - b}{2 + 2\alpha} × (\frac{3\alpha + b}{2 + 2\alpha})^3}{\frac{1 - \alpha}{2 + 2\alpha} × \frac{1 - \alpha - b}{2 + 2\alpha}} = \frac{(\alpha - b) × (3\alpha + b)^3}{(1 - \alpha) × (1 - \alpha - b) × (2 + 2\alpha)^2}。$其他条件不变,$H_2O(g) $起始量增加到 5 mol,则平衡时n(总$) = 1 mol + 5 mol + 2\alpha mol = 7.8 mol,$$n(H_2) = (3\alpha + b) mol = (3 × 0.90 + 0.65) mol = 3.35 mol,$则$H_2(g) $的物质的量分数为$\frac{3.35 mol}{7.8 mol} × 100\% \approx 43\%。$
(3)氢氧燃料电池中,氢气失电子发生氧化反应,故在负极发生反应。
(4)在允许$O^{2-} $自由迁移的固体电解质燃料电池中,$C_nH_{2n + 2} $在负极被氧化结合$O^{2-} $生成$CO_2 $和$H_2O,$电极反应式为$C_nH_{2n + 2} - (6n + 2)e^- + (3n + 1)O^{2-} \xlongequal{} nCO_2 + (n + 1)H_2O。$
(5)由图示可知,吸附在催化剂表面的甲醇分子逐步脱氢得到CO,且能垒越低,活化能越小,越容易进行,所以最可行的途径为$a \rightarrow b \rightarrow e \rightarrow h \rightarrow j。$
$(2)①BC ②\frac{(\alpha - b) × (3\alpha + b)^3}{(1 - \alpha) × (1 - \alpha - b) × (2 + 2\alpha)^2} 43\% $
(3)负
$(4)C_nH_{2n + 2} - (6n + 2)e^- + (3n + 1)O^{2-} \xlongequal{} nCO_2 + (n + 1)H_2O $
$(5)b \rightarrow e \rightarrow h \rightarrow j $
【解析】燃烧热、盖斯定律、化学平衡的移动、化学平衡常数的计算、电极反应式书写
(1)根据题目信息写出热化学方程式:
$①H_2(g) + \frac{1}{2}O_2(g) \xlongequal{} H_2O(g) \Delta H_1 = -242 kJ/mol,$
$②H_2O(l) \xlongequal{} H_2O(g) \Delta H_2 = +44 kJ/mol,$$H_2 $燃烧热指$ 1 mol H_2 $完全燃烧生成$H_2O(l) $放出的热量,根据盖斯定律可得出$H_2(g) + \frac{1}{2}O_2(g) \xlongequal{} H_2O(l) \Delta H = \Delta H_1 - \Delta H_2 = -286 kJ/mol。$
(2)①增加甲烷用量会增大$H_2O(g) $的平衡转化率,甲烷平衡转化率减小,A错误;恒温恒压下通入惰性气体,使得体系中各物质浓度减小,其结果等效于减小压强,平衡向气体分子数增加的方向移动,即反应Ⅰ平衡正向移动,甲烷平衡转化率增大,B正确;移除一氧化碳可使反应Ⅰ平衡正向移动,甲烷平衡转化率增大,C正确;加入催化剂可加快反应速率,缩短达到平衡的时间,不会引起平衡移动,甲烷平衡转化率不变,D错误。②两个反应的转化量表示如下:
$Ⅰ CH_4(g) + H_2O(g) \rightleftharpoons CO(g) + 3H_2(g) $
$\Delta n \alpha mol \alpha mol \alpha mol 3\alpha mol $
$Ⅱ CO(g) + H_2O(g) \rightleftharpoons CO_2(g) + H_2(g) $
$\Delta n b mol b mol b mol b mol $
反应Ⅱ气体物质的量不变,气体总物质的量的变化由反应Ⅰ引起,平衡时n(总$) = (2 + 2\alpha) mol,$$n(CH_4) = (1 - \alpha) mol,$$n(H_2O) = (1 - \alpha - b) mol,$$n(CO) = (\alpha - b) mol,$$n(H_2) = (3\alpha + b) mol,$
反应Ⅰ的平衡常数$K_x = \frac{x(CO) × x^3(H_2)}{x(CH_4) × x(H_2O)} = \frac{\frac{\alpha - b}{2 + 2\alpha} × (\frac{3\alpha + b}{2 + 2\alpha})^3}{\frac{1 - \alpha}{2 + 2\alpha} × \frac{1 - \alpha - b}{2 + 2\alpha}} = \frac{(\alpha - b) × (3\alpha + b)^3}{(1 - \alpha) × (1 - \alpha - b) × (2 + 2\alpha)^2}。$其他条件不变,$H_2O(g) $起始量增加到 5 mol,则平衡时n(总$) = 1 mol + 5 mol + 2\alpha mol = 7.8 mol,$$n(H_2) = (3\alpha + b) mol = (3 × 0.90 + 0.65) mol = 3.35 mol,$则$H_2(g) $的物质的量分数为$\frac{3.35 mol}{7.8 mol} × 100\% \approx 43\%。$
(3)氢氧燃料电池中,氢气失电子发生氧化反应,故在负极发生反应。
(4)在允许$O^{2-} $自由迁移的固体电解质燃料电池中,$C_nH_{2n + 2} $在负极被氧化结合$O^{2-} $生成$CO_2 $和$H_2O,$电极反应式为$C_nH_{2n + 2} - (6n + 2)e^- + (3n + 1)O^{2-} \xlongequal{} nCO_2 + (n + 1)H_2O。$
(5)由图示可知,吸附在催化剂表面的甲醇分子逐步脱氢得到CO,且能垒越低,活化能越小,越容易进行,所以最可行的途径为$a \rightarrow b \rightarrow e \rightarrow h \rightarrow j。$
查看更多完整答案,请扫码查看


