第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
例1
计算:
(1) $-20 + (-14) - (-18) - 13$;
(2) $-1^{2024} - \frac{1}{2} ÷ 3 × |3 - (-3)^2|$。
(3) $\frac{11}{5} × (\frac{1}{3} - \frac{1}{2}) × \frac{3}{11} ÷ \frac{5}{4}$;
(4) $-4^2 - (-1)^{10} × | - 3 | ÷ \frac{3}{16}$。
计算:
(1) $-20 + (-14) - (-18) - 13$;
(2) $-1^{2024} - \frac{1}{2} ÷ 3 × |3 - (-3)^2|$。
(3) $\frac{11}{5} × (\frac{1}{3} - \frac{1}{2}) × \frac{3}{11} ÷ \frac{5}{4}$;
(4) $-4^2 - (-1)^{10} × | - 3 | ÷ \frac{3}{16}$。
答案:
(1)-29;(2)-2;(3)$-\dfrac{2}{25}$;(4)-32.
1. 已知 $|ab - 2| + (b - 1)^2 = 0$,求 $\frac{1}{ab} + \frac{1}{(a + 1)(b + 1)} + \frac{1}{(a + 2)(b + 2)} + … + \frac{1}{(a + 2022)(b + 2022)}$ 的值。
答案:
$\dfrac{2023}{2024}$.
例2
观察并探求规律:
$\frac{1}{2}, -\frac{2}{3}, \frac{3}{4}, -\frac{4}{5}, \frac{5}{6}, -\frac{6}{7}, …$。
(1) 写出第 $7, 8, 9$ 个数;
(2) 第 $2022$ 个数是多少?
分析 通过观察得到该列数的奇次项为正数,偶次项为负数,且每个数的分子均比分母小 $1$,根据此规律解决问题。
观察并探求规律:
$\frac{1}{2}, -\frac{2}{3}, \frac{3}{4}, -\frac{4}{5}, \frac{5}{6}, -\frac{6}{7}, …$。
(1) 写出第 $7, 8, 9$ 个数;
(2) 第 $2022$ 个数是多少?
分析 通过观察得到该列数的奇次项为正数,偶次项为负数,且每个数的分子均比分母小 $1$,根据此规律解决问题。
答案:
(1)$\dfrac{7}{8}$,$-\dfrac{8}{9}$,$\dfrac{9}{10}$.(2)$-\dfrac{2022}{2023}$.
2. 由 $a_2 = \frac{1}{1 - a_1}, a_3 = \frac{1}{1 - a_2}, …$,可得 $a_n = \frac{1}{1 - a_{n - 1}}(n \geq 2$,且 $n$ 为整数)。依此类推,当 $a_1 = 2$ 时,则 $a_{2020}$ 的值为( )
A.$2$
B.$-1$
C.$\frac{1}{2}$
D.$0$
A.$2$
B.$-1$
C.$\frac{1}{2}$
D.$0$
答案:
A
例3
某检修小组开车从 $A$ 地出发,在东西方向的马路上检修线路. 如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下表(单位:$km$)。
|第一次|第二次|第三次|第四次|第五次|第六次|第七次|
|$-3$| $+8$| $-9$| $+10$| $+4$| $-6$| $-2$|
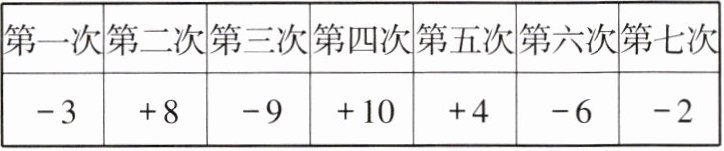
(1) 求检修小组收工时距 $A$ 地有多远;
(2) 检修小组第______次距 $A$ 地最远;
(3) 若开车每千米耗油 $0.3\ L$,则共耗油多少升?
分析 (1) 根据有理数的加法可得;
(2) 根据有理数的加法,可以得到每次距离 $A$ 地的距离,再根据有理数的大小比较可得;(3) 根据单位耗油量乘行驶的路程等于总耗油量可得。
某检修小组开车从 $A$ 地出发,在东西方向的马路上检修线路. 如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下表(单位:$km$)。
|第一次|第二次|第三次|第四次|第五次|第六次|第七次|
|$-3$| $+8$| $-9$| $+10$| $+4$| $-6$| $-2$|

(1) 求检修小组收工时距 $A$ 地有多远;
(2) 检修小组第______次距 $A$ 地最远;
(3) 若开车每千米耗油 $0.3\ L$,则共耗油多少升?
分析 (1) 根据有理数的加法可得;
(2) 根据有理数的加法,可以得到每次距离 $A$ 地的距离,再根据有理数的大小比较可得;(3) 根据单位耗油量乘行驶的路程等于总耗油量可得。
答案:
(1)2 km. (2)五 (3)12.6 L.
查看更多完整答案,请扫码查看


