《2025年新课程实践与探究丛书七年级数学上册人教版》

例1 计算：
(1)$-7^{2}+2× (-3)^{2}+(-6)÷ \left(-\dfrac{1}{3}\right)^{2}$；
(2)$\left[\left(1-\dfrac{1}{3}\right)^{2}-\left(-1\dfrac{2}{3}\right)÷ \left(-\dfrac{9}{8}\right)\right]× \left(-1\dfrac{1}{2}\right)^{3}$；
(3)$-1^{2024}-[2 - (-1)^{2024}]÷ \left(-\dfrac{2}{5}\right)× \dfrac{5}{2}$.

答案： （1）$-85$；（2）$\dfrac{7}{2}$；（3）$\dfrac{21}{4}$．

1. 计算：
(1)$\left(\dfrac{1}{2}-\dfrac{2}{3}\right)× (-12)-|-2 + 5|÷ \left(1-\dfrac{1}{4}\right)$；
(2)$-1^{2024}+(-2)^{4}× \left(-\dfrac{1}{2}\right)+(-9)÷ (-1)$.

答案： （1）$-2$；（2）$0$．

例2 观察下列三行数：
$2$,$-4$,$8$,$-16$,$32$,…$$；①
$-1$,$2$,$-4$,$8$,$-16$,…$$；②
$3$,$-3$,$9$,$-15$,$33$,…$$. ③
(1)第①行数有什么规律？
(2)第②③行数与第①行数分别有什么关系？
(3)取每行数的第 9 个数,计算这三个数的和.

答案： （1）后一个数是前一个数乘$-2$得到的．
（2）第②行每个数乘$-2$得到第①行所对应的数，第③行每个数减$1$得到第①行所对应的数．
（3）$769$．

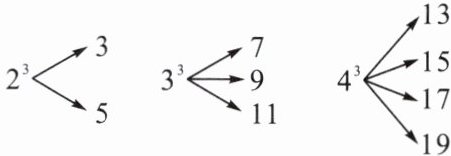
2. 一个自然数的立方,可以“分裂”成若干个连续奇数的和. 例如$2^{3}$,$3^{3}$,$4^{3}$分别可以按如图所示的方式“分裂”成 2 个、3 个、4 个连续奇数的和,即$2^{3}= 3 + 5$,$3^{3}= 7 + 9 + 11$,$4^{3}= 13 + 15 + 17 + 19$. 若$6^{3}$也按照此规律进行“分裂”,则$6^{3}$“分裂”出的奇数中,最大的是( )


A.37
B.39
C.41
D.43

答案： C