《2025年新课堂学习与探究九年级数学全一册北师大版》

5. 关于方程$88(x - 2)^{2}= 95$的两个根,下列说法正确的是(A)。
A.一个根小于$1$,另一个根大于$3$
B.一个根小于$-2$,另一个根大于$2$
C.两个根都小于$0$
D.两个根都大于$2$

答案： A

6. 方程$x^{2}+x - 1 = 0的根精确到0.1$的近似解是(B)。
A.$0.6$,$1.6$
B.$0.6$,$-1.6$
C.$-0.6$,$1.6$
D.$-0.6$,$-1.6$

答案： B

7. $6月6$日是全国爱眼日,每个人都要注意用眼卫生。假设一个人患了红眼病,经过两轮传染后,共有$144$人患病,每轮传染中平均一个人传染的人数为(B)。
A.$10$
B.$11$
C.$12$
D.$13$

答案： B

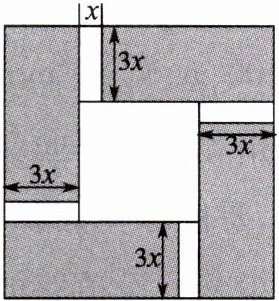
8. 某景区准备在一块边长为$20m$的大正方形花园中间修建一个正方形的休闲场所,如图所示,要求修建$4$条等宽的矩形小道连接两个正方形的四边。若小道的长是宽的$3$倍,且花草种植区域(阴影部分)的面积为$192m^{2}$,设小道宽度为$x m$,根据题意列出关于$x$的一元二次方程是4×3x(20-4x)=192。

答案： 4×3x(20-4x)=192

9. 如图,小明同学用一张长为$11cm$、宽为$7cm的矩形纸板制作一个底面积为21cm^{2}$的无盖长方体纸盒。他在纸板的$4个角各剪去1$个同样大小的正方形,然后将剩下部分四周向上折叠即可(损耗不计)。求剪去的正方形的边长。

答案： 解:设剪去的正方形的边长为x cm.(11-2x)(7-2x)=21,整理得x²-9x+14=0,解得x=2或7(舍去).答:剪去的正方形的边长为2 cm.

10. 已知关于$x的方程(2k + 1)x^{2}-4kx + k - 1 = 0$。
(1) 当$k$为何值时,这个方程是一元一次方程？求出这个一元一次方程的根。
(2) 当$k$为何值时,这个方程是一元二次方程？写出这个一元二次方程的二次项系数、一次项系数和常数项。

答案： $(1)$ 当方程是一元一次方程时
解：对于一元一次方程，其二次项系数为$0$，即$2k + 1 = 0$，
解方程$2k+1 = 0$，移项可得$2k=-1$，解得$k =-\frac{1}{2}$。
将$k =-\frac{1}{2}$代入原方程，原方程变为$-4×(-\frac{1}{2})x+(-\frac{1}{2}) - 1 = 0$，
即$2x-\frac{3}{2}=0$，移项得$2x=\frac{3}{2}$，解得$x=\frac{3}{4}$。
$(2)$ 当方程是一元二次方程时
解：对于一元二次方程，其二次项系数不为$0$，即$2k + 1\neq0$，解得$k\neq-\frac{1}{2}$。
此时二次项系数为$2k + 1$，一次项系数为$-4k$，常数项为$k - 1$。
综上，$(1)$当$k =-\frac{1}{2}$时，方程是一元一次方程，根为$x = \frac{3}{4}$；$(2)$当$k\neq-\frac{1}{2}$时，方程是一元二次方程，二次项系数$2k + 1$，一次项系数$-4k$，常数项$k - 1$。

11. 现有两个正方形,小正方形的边长比大正方形的边长的一半多$1cm$,大正方形的面积比小正方形的面积的$2倍多4cm^{2}$。
(1) 若求大正方形的边长,怎样列方程？列出方程,并化为一般形式。
(2) 若设大正方形的边长为$x cm$,$x会小于0$吗？$x会小于4$吗？$x会大于10$吗？
(3) 完成下表：
| $x$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| | | | | | | |

(4) 你能由上表求出大正方形的边长吗？
（1）设大正方形的边长为$x cm$，则小正方形的边长为$(\frac{x}{2}+1)cm$。根据题意可列方程：$x^{2}=2(\frac{x}{2}+1)^{2}+4$。化为一般形式：先展开$(\frac{x}{2}+1)^{2}=\frac{x^{2}}{4}+x + 1$，则$x^{2}=2(\frac{x^{2}}{4}+x + 1)+4$，去括号得$x^{2}=\frac{x^{2}}{2}+2x + 2 + 4$，移项得$x^{2}-\frac{x^{2}}{2}-2x - 6 = 0$，合并同类项得$\frac{x^{2}}{2}-2x - 6 = 0$，两边同乘$2$得$x^{2}-4x - 12 = 0$。
（2）$x$不会小于$0$，因为边长不能为负；$x$不会小于$4$；$x$不会大于$10$。
（3）表格第二行依次填$-7$，$0$，$9$，$20$，$33$，$48$。
（4）能，大正方形的边长为$6cm$。

答案： （1）
设大正方形的边长为$x cm$，则小正方形的边长为$(\frac{x}{2}+1)cm$。
根据大正方形的面积比小正方形的面积的$2$倍多$4cm^{2}$，可列方程：
$x^{2}=2(\frac{x}{2}+1)^{2}+4$。
化为一般形式：
先展开$(\frac{x}{2}+1)^{2}=\frac{x^{2}}{4}+x + 1$，则$x^{2}=2(\frac{x^{2}}{4}+x + 1)+4$。
去括号得$x^{2}=\frac{x^{2}}{2}+2x + 2 + 4$。
移项得$x^{2}-\frac{x^{2}}{2}-2x - 6 = 0$。
合并同类项得$\frac{x^{2}}{2}-2x - 6 = 0$，两边同乘$2$得$x^{2}-4x - 12 = 0$。
（2）
$x$表示大正方形的边长，边长不能为负，所以$x$不会小于$0$。
当$x = 4$时，小正方形边长$\frac{4}{2}+1=3$，大正方形面积$4^{2}=16$，小正方形面积$3^{2}=9$，$2×9 + 4=22\neq16$，且由$x^{2}-4x - 12 = 0$，$(x - 6)(x + 2)=0$，根为$x = 6$或$x=-2$，从函数$y=x^{2}-4x - 12=(x - 2)^{2}-16$，对称轴$x = 2$，当$x\lt6$时，$y\lt0$，所以$x$不会小于$4$（因为$x$要满足方程$x^{2}-4x - 12 = 0$的实际意义）。
当$x = 10$时，$x^{2}=100$，小正方形边长$\frac{10}{2}+1 = 6$，小正方形面积$36$，$2×36+4 = 76\neq100$，把$x = 10$代入$x^{2}-4x - 12$得$100-40 - 12 = 48\gt0$，但从方程$(x - 6)(x + 2)=0$，所以$x$不会大于$10$。
（3）
表格第二行依次填$-7$，$0$，$9$，$20$，$33$，$48$。
（4）
能，由$x^{2}-4x - 12 = 0$，$(x - 6)(x + 2)=0$，且$x\gt0$，所以大正方形边长$x = 6cm$。