《2025年启东中学作业本七年级数学上册苏科版连淮专版》

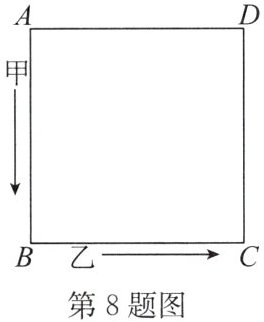
8. (2024·清江浦区开学) 如图,沿着边长为 $90$ 米的正方形,按 $A→B→C→D→A…$ 方向,甲从点 $A$ 以 $63$ 米/分的速度,乙从点 $B$ 以 $72$ 米/分的速度同时行走,当乙第一次追上甲时是在正方形的某个顶点处,则这个顶点是(B)

A.顶点 $A$
B.顶点 $B$
C.顶点 $C$
D.顶点 $D$

答案： B

9. 某工厂用两辆车运货,从产地运往工厂,甲车的速度是 $40$ km/h,开出半小时后,乙车也从产地开出,它的速度是 $50$ km/h,结果两车同时到达工厂. 那么产地和工厂间的路程为100 km.

答案： 100 km

10. 已知某铁路桥长 $1500$ 米. 现有一列火车从桥上通过,测得火车从开始上桥到完全过桥共用 $90$ 秒,整列火车完全在桥上的时间是 $60$ 秒. 则这列火车长为300米.

答案： 300

11. 从 $A$ 地到 $B$ 地是一段总长为 $180$ 千米,先上坡、再下坡的公路. 一辆汽车从 $A$ 地驶往 $B$ 地后再原路返回 $A$ 地,汽车在上坡时的速度为 $30$ 千米/时,下坡时的速度为 $40$ 千米/时,从 $A$ 地驶往 $B$ 地所需时间比从 $B$ 地驶往 $A$ 地所需时间多 $0.5$ 小时,求从 $A$ 地驶往 $B$ 时上坡和下坡的路程.

答案： 解:设从A地驶往B地时,上坡的路程为x千米,则下坡的路程为$(180-x)$千米.根据题意,得$(\frac{x}{30}+\frac{180-x}{40})-(\frac{180-x}{30}+\frac{x}{40})=0.5$,解得$x=120$,则$180-x=60$.答:从A地驶往B地时,上坡的路程为120千米,下坡的路程为60千米.

12. 受第 $24$ 届北京冬季奥林匹克运动会的影响,小勇爱上了雪上运动. 一天,小勇在滑雪场训练滑雪,第一次他从滑雪道 $A$ 端以 $(x + 2)$ 米/秒的平均速度滑到 $B$ 端,用了 $24$ 秒；第二次从滑雪道 $A$ 端以 $(x + 3)$ 米/秒的平均速度滑到 $B$ 端,用了 $20$ 秒.
(1) 求 $x$ 的值；
(2) 设小勇从滑雪道 $A$ 端滑到 $B$ 端的平均速度为 $v$ 米/秒,所用时间为 $t$ 秒,请用含 $t$ 的代数式表示 $v$. (不要求写出 $t$ 的取值范围)

答案： 解:
(1)根据题意,得$24(x+2)=20(x+3)$,解得$x=3$.
(2)从滑雪道A端滑到B端的路程为$24×(3+2)=120$(米).因为小勇从滑雪道A端滑到B端的平均速度为v米/秒,所用时间为t秒,所以$v=\frac{120}{t}$.

13. 甲、乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快 $200$ 米,两人同时从起点出发,同向而行,经过 $3$ 分钟两人首次相遇,此时乙还需跑 $150$ 米才能跑完第一圈.
(1) 求甲、乙两人的速度分别是每分钟多少米；
(2) 若两人相遇后,甲立即以每分钟 $300$ 米的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过 $1.2$ 分钟两人再次相遇,则乙的速度至少每分钟要提高多少米？

答案： 解:
(1)设乙的速度是每分钟x米,则甲的速度是每分钟$(x+200)$米.根据题意,得$3(x+200)-3x=3x+150$,解得$x=150$.$150+200=350$(米).答:甲的速度是每分钟350米,乙的速度是每分钟150米.
(2)设乙的速度至少每分钟要提高y米.根据
(1)可知,跑道的长度为$150×3+150=600$(米).根据题意,得$1.2(300+150+y)=600$,解得$y=50$.答:乙的速度至少每分钟要提高50米.