《2025年启东中学作业本七年级数学上册苏科版连淮专版》

10. 按规律排列的一列数：$0$,$6$,$16$,$30$,$48$,…,则第$n$个数为2(n²-1).(用含$n$的代数式表示)

答案： 2(n²-1)

11. (1)一本笔记本原价$a$元,降价后比原来便宜了$b$元,小玲买了$3$本这样的笔记本,共花了3(a-b)元；
(2)某商品进价为$a$元,商店将其价格提高$30\%$作为零售价销售,在销售旺季过后,商店又以$8$折(即售价的$80\%$)优惠开展促销活动,这时一件商品的售价为1.04a元.

答案：
(1)3(a-b)
(2)1.04a

12. 某养殖公司为了控制南美白对虾质量,建立了严格的对虾品质标准,将养殖对虾分成了$12$个等级,$1$级虾的品质最好,$2$级次之,依此类推,第$12$级品质最差,在销售南美白对虾时,制定销售价格如下：第$6级的对虾售价为40$元/千克,从第$6$级起,品质每提升$1$级,每千克的售价将提升$3$元；品质每下降$1$级,每千克的售价将降低$2$元.
(1)$3$级虾的售价为49元/千克；$10$级虾的售价为32元/千克.
(2)若对虾的等级为$n$,用含$n$的代数式表示该等级的售价：
①当$n＜6$时,售价为(58-3n)元/千克；②当$n＞6$时,售价为(52-2n)元/千克.
(3)水产老板小李计划在该养殖公司购进$2级南美白对虾400$千克,养殖公司负责送货上门,但要收$200$元的运费.因为小李是养殖公司的老客户,负责人给出了如下两种优惠方案：
方案一：降价$5\%$,并减免全部运费；方案二：降价$8\%$,但运费不减.请你帮小李计算哪种优惠方案更加合算.
解:2级南美白对虾的售价为40+(6-2)×3=52(元/千克),方案一所需费用为52×400×(1-5%)=19760(元),方案二所需费用为52×400×(1-8%)+200=19336(元),因为19336＜19760,所以方案二更加合算.

答案：
(1)49 32
(2)①(58-3n) ②(52-2n)
(3)解:2级南美白对虾的售价为40+(6-2)×3=52(元/千克),方案一所需费用为52×400×(1-5%)=19760(元),方案二所需费用为52×400×(1-8%)+200=19336(元),因为19336＜19760,所以方案二更加合算.

13. (2024·海门市月考)如图①是一个长为$2m$,宽为$2n$的长方形,沿图中虚线用剪刀均分成$4$个小长方形,然后按图②的方式拼成一个正方形.

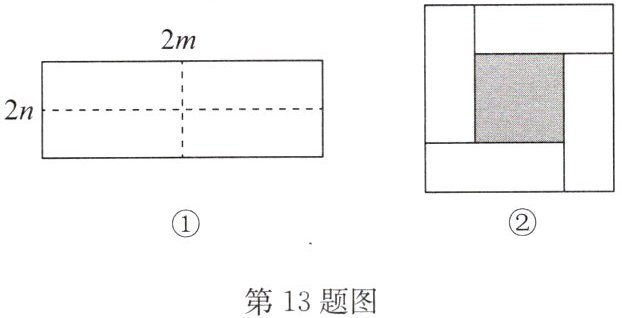
(1)图②中的阴影部分的正方形的边长等于m-n.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①：(m-n)²；方法②：(m+n)²-4mn.
(3)观察图②,你能写出$(m + n)^{2}$,$(m - n)^{2}$,$mn$这三个代数式之间的等量关系吗？
解:这三个代数式之间的等量关系是(m-n)²=(m+n)²-4mn.

答案： m-n
@@
(2)(m-n)² (m+n)²-4mn
(3)解:这三个代数式之间的等量关系是(m-n)²=(m+n)²-4mn.