《2025年名校课堂七年级数学上册人教版福建专版》

11. 湖南师大附中校本经典题 若单项式$x^{a + 2}y^{2}$与$3xy^{b}$的和是单项式，则$a^{b}$的值是(D)

A.$-2$
B.$2$
C.$-1$
D.$1$

答案： D

12. 若关于$x$，$y$的多项式$x^{2}+3kxy - 3y^{2}-\frac{1}{3}xy - 8$不含$xy$项，则$k$的值为1/9.

答案： 1/9

13. 若$x - y = 3$，则整式$\frac{1}{4}(x - y)^{2}-0.3(x - y)+0.75(x - y)^{2}+\frac{3}{10}(x - y)-2(x - y)+7$的值为10.

答案： 10

14. 先合并同类项，再求值：$\frac{1}{4}a^{2}b - 0.4ab^{2}-\frac{1}{2}a^{2}b+\frac{2}{5}ab^{2}-1$，其中$a = 2$，$b = -1$.

答案： 解:原式$=(\frac{1}{4}a^{2}b-\frac{1}{2}a^{2}b)+(-0.4ab^{2}+\frac{2}{5}ab^{2})-1=-\frac{1}{4}a^{2}b-1$.当$a=2$,$b=-1$时,原式$=-\frac{1}{4}×2^{2}×(-1)-1=0$.

15. 如图，一个长方形游乐场的长为$6x$m，宽为$2y$m，其中半圆形A区为休息区、长方形B区为游泳区，其他区域是绿化草地.已知半圆形A区的直径和长方形B区的宽都是$y$m，B区的长是$3x$m.
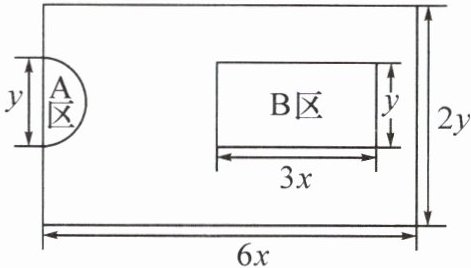
(1)用代数式分别表示该游乐场休息区与游泳区的面积(结果保留$\pi$).
(2)当$x = 15$，$y = 20$时，若绿化草地每平方米需要费用$50$元，求这个游乐场绿化草地的费用($\pi$取$3$).

答案： 解:
(1)休息区的面积为$\frac{1}{2}×π×(\frac{y}{2})^{2}=\frac{π}{8}y^{2}(m^{2})$;游泳区的面积为$3xy\ m^{2}$.
(2)绿化草地的面积为$6x·2y-\frac{π}{8}y^{2}-3xy=12xy-\frac{π}{8}y^{2}-3xy=(9xy-\frac{π}{8}y^{2})m^{2}$.因为$x=15$,$y=20$,所以绿化草地的面积为$9×15×20-\frac{3}{8}×20^{2}=2700-150=2550(m^{2})$.所以绿化草地的费用为$2550×50=127500$(元).

16. 北京四中校本经典题 有这样一道题：当$a = 2024$，$b = -2025$时，求多项式$7a^{3}-6a^{3}b + 3a^{2}b+3a^{3}+6a^{3}b - 3a^{2}b - 10a^{3}+2023$的值.
小明说：“本题中‘$a = 2024$，$b = -2025$’是多余的条件.”小强马上反对说：“这不可能，多项式中含有$a$和$b$，不给出$a$，$b$的值，怎么能求出多项式的值呢?”你同意哪名同学的观点? 请说明理由.

答案： 解:同意小明的观点.理由如下:原式$=(7a^{3}+3a^{3}-10a^{3})+(-6a^{3}b+6a^{3}b)+(-3a^{2}b+3a^{2}b)+2023=2023$.
∴该多项式的值与$a$,$b$的取值无关.
∴小明的观点正确.

17. 多项式$m - 3m + 5m - 7m+\cdots - 99m$合并同类项的结果为(B)

A.$-100m$
B.$-50m$
C.$-200m$
D.$-150m$

答案： B