第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
3. 快车和慢车分别从相距 200 km 的甲、乙两地出发,相向而行,慢车比快车晚出发 2 h(慢车出发时快车还未到乙地)。快车到达乙地后不停留,直接按原路返回甲地。快车出发 4 h 后,快车第二次遇到慢车。已知快车每小时比慢车多行驶 20 km,则慢车的速度为
60
km/h。
答案:
3.60
方法 2 列表格分析法
【例 2】学校组织植树活动,已知在甲地植树的有 23 人,在乙地植树的有 17 人。现调 20 人去支援甲、乙两地,使在甲地植树的人数是在乙地植树人数的 2 倍,则应调往甲、乙两地各多少人?
【分析】列出表格,可将复杂的数量关系直观地呈现出来(x表示调往甲地的人数)。
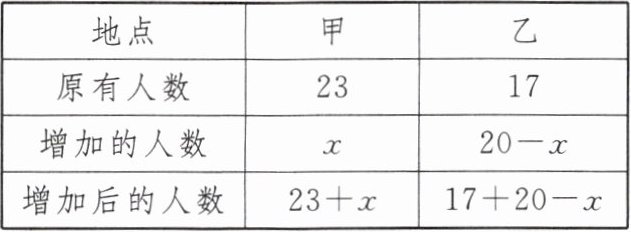
等量关系是甲地增加后的人数 = 2 × 乙地增加后的人数。
【例 2】学校组织植树活动,已知在甲地植树的有 23 人,在乙地植树的有 17 人。现调 20 人去支援甲、乙两地,使在甲地植树的人数是在乙地植树人数的 2 倍,则应调往甲、乙两地各多少人?
【分析】列出表格,可将复杂的数量关系直观地呈现出来(x表示调往甲地的人数)。

等量关系是甲地增加后的人数 = 2 × 乙地增加后的人数。
答案:
解:设调往甲地的人数为$x$,则调往乙地的人数为$20 - x$。
根据题意,得:
$23 + x = 2×(17 + 20 - x)$
解方程:
$23 + x = 2×(37 - x)$
$23 + x = 74 - 2x$
$x + 2x = 74 - 23$
$3x = 51$
$x = 17$
调往乙地的人数为:$20 - x = 20 - 17 = 3$
答:应调往甲地17人,调往乙地3人。
根据题意,得:
$23 + x = 2×(17 + 20 - x)$
解方程:
$23 + x = 2×(37 - x)$
$23 + x = 74 - 2x$
$x + 2x = 74 - 23$
$3x = 51$
$x = 17$
调往乙地的人数为:$20 - x = 20 - 17 = 3$
答:应调往甲地17人,调往乙地3人。
4. 温州厂和杭州厂同时生产某种型号的机器若干台,温州厂可支援外地 10 台,杭州厂可支援外地 4 台。现在决定给武汉 8 台,给南昌 6 台,每台机器的运费(单位:元)如下表:
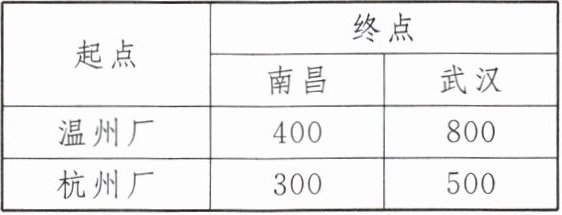
设杭州厂运往南昌的机器为 x 台。
(1) 用含 x 的式子表示总运费。
(2) 若总运费为 8400 元,求杭州厂运往南昌的机器为多少台。
(3) 试问有没有可能使总运费是 7800 元?若有可能,请写出相应的调运方案;若没有可能,请说明理由。

设杭州厂运往南昌的机器为 x 台。
(1) 用含 x 的式子表示总运费。
(2) 若总运费为 8400 元,求杭州厂运往南昌的机器为多少台。
(3) 试问有没有可能使总运费是 7800 元?若有可能,请写出相应的调运方案;若没有可能,请说明理由。
答案:
(1)设杭州厂运往南昌的机器为$x$台,则杭州厂运往武汉的机器为$(4 - x)$台,温州厂运往南昌的机器为$(6 - x)$台,温州厂运往武汉的机器为$\lbrack 10 - (6 - x)\rbrack = (4 + x)$台。
总运费$y = 300x + 500(4 - x) + 400(6 - x) + 800(4 + x)$
$= 300x + 2000 - 500x + 2400 - 400x + 3200 + 800x$
$= (200x + 7600)$元
其中$0\leq x\leq4$的整数。
(2)当$y = 8400$时,
$200x + 7600 = 8400$
$200x = 800$
$x = 4$
答:杭州厂运往南昌的机器为$4$台。
(3)当$y = 7800$时,
$200x + 7600 = 7800$
$200x = 200$
$x = 1$
答:有可能,杭州厂运往南昌$1$台,运往武汉$3$台,温州厂运往南昌$5$台,运往武汉$5$台。
(1)设杭州厂运往南昌的机器为$x$台,则杭州厂运往武汉的机器为$(4 - x)$台,温州厂运往南昌的机器为$(6 - x)$台,温州厂运往武汉的机器为$\lbrack 10 - (6 - x)\rbrack = (4 + x)$台。
总运费$y = 300x + 500(4 - x) + 400(6 - x) + 800(4 + x)$
$= 300x + 2000 - 500x + 2400 - 400x + 3200 + 800x$
$= (200x + 7600)$元
其中$0\leq x\leq4$的整数。
(2)当$y = 8400$时,
$200x + 7600 = 8400$
$200x = 800$
$x = 4$
答:杭州厂运往南昌的机器为$4$台。
(3)当$y = 7800$时,
$200x + 7600 = 7800$
$200x = 200$
$x = 1$
答:有可能,杭州厂运往南昌$1$台,运往武汉$3$台,温州厂运往南昌$5$台,运往武汉$5$台。
查看更多完整答案,请扫码查看


