《2025年名校课堂七年级数学上册人教版福建专版》

1. 如果正方形的边长为a，那么它的周长l=4a，面积S=$a^{2}$；当a=5 cm时，l=20cm，S=25cm².

答案： 4a $a^{2}$ 20 25

2. 若一个长方形的宽为b，长比宽多3，则这个长方形的面积S=$b(b+3)$；当b=3 cm时，S=18cm².

答案： $b(b+3)$ 18

3. 一个火炬模型的底座可以近似看作圆锥。如果V，r，h分别表示圆锥体积、底面半径和圆锥的高，那么V=$\frac{1}{3}\pi r^{2}h$；当r=3 m，h=12 m时，V=108m³(π取3)。

答案： $\frac{1}{3}\pi r^{2}h$ 108

4. 甲车从A地出发以60 km/h的速度沿公路匀速行驶0.5 h后，乙车也从A地出发，以80 km/h的速度沿该公路与甲车同向匀速行驶。乙车出发x h后，甲车离开A地的路程用代数式表示为(60x+30)km，乙车离开A地的路程用代数式表示为80xkm；当x=5时，甲车离开A地的路程为330km，乙车离开A地的路程为400km。

答案： (60x+30) 80x 330 400

5. 兰生复旦校本经典题 如图，一枚玉璧的形状可看作一个圆环，外圆与内圆的半径分别是R和r.
（1）用代数式表示圆环面积.
（2）当R=5 cm，r=2 cm时，圆环的面积是多少（π取3.14）？

答案： 解:
(1)圆环的面积为$(\pi R^{2}-\pi r^{2})cm^{2}$.
(2)当$R=5\ cm,r=2\ cm$时,$\pi R^{2}-\pi r^{2}=3.14×5^{2}-3.14×2^{2}=65.94(cm^{2})$.因此,圆环的面积是$65.94\ cm^{2}$.

6. 石家庄外国语校本经典题 如图，已知长方体的高为h，底面是边长为a的正方形.
（1）请写出用a和h表示长方体的体积V和表面积S的代数式.
（2）当h=3，a=2时，请分别求出长方体的体积V和表面积S的值.

答案： 解:
(1)$V=a^{2}h$,$S=2a^{2}+4ah$.
(2)当$h=3$,$a=2$时,$V=a^{2}h=2^{2}×3=12$,$S=2a^{2}+4ah=2×2^{2}+4×2×3=32$.

7. 小明周末从家里去书店，需要先步行一段路程，然后再坐公交车到书店，步行的速度为4千米/时，公交车的速度为45千米/时。小明先步行x分钟，再乘车y分钟，则小明家离书店的路程是($\frac{1}{15}x+\frac{3}{4}y$)千米；当x=45，y=10时，小明家离书店的路程是10.5千米.

答案： ($\frac{1}{15}x+\frac{3}{4}y$) 10.5

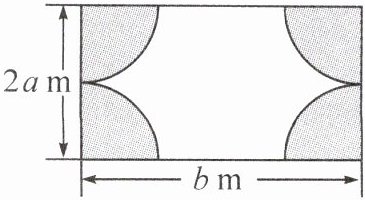
8. 如图，这是某居民小区的一块宽为2a m，长为b m的长方形空地，为了美化环境，准备在这块长方形空地的四个顶点处各修建一个半径为a m的扇形花台，然后在花台内种花，其余空地种草.
（1）用代数式表示种草的面积.
（2）当a=10，b=35时，求种草的面积（π取3.14）.

答案： 解:
(1)由题意,得种草的面积为$(2ab-\pi a^{2})m^{2}$.
(2)当$a=10$,$b=35$时,$2ab-\pi a^{2}=2×10×35-3.14×10^{2}=2×10×35-3.14×100=700-314=386$.
答:种草的面积为$386\ m^{2}$.