《2025年名校课堂七年级数学上册人教版福建专版》

9. 一个两位数,十位上的数字是个位数字的 $ 2 $ 倍,将个位数字与十位数字调换,得到一个新的两位数,这两个两位数的和是 $ 132 $.设原两位数的个位数字为 $ x $,可列方程为(10×2x+x)+(10x+2x)=132.

答案： (10×2x+x)+(10x+2x)=132

10. (2023·福州十九中期末节选)福州盆地盛产柑橘,福橘是福州市市果,汁多味甜,风味独特.某销售商为了扩大福橘销售量,开设实体店和线上两种销售渠道,包装方式及售价如下表所示.假没用这两种包装方式恰好包装完所有的福橘.

(1)销售商第一批购进 $ 1000 $ kg 福橘全部售卖完毕,已知实体店比线上少卖 $ 40 $ 盒,则实体店和线上各售出多少盒?
(2)已知实体店需要支付人工、房租等额外成本,每售卖一盒礼盒装,有 $ 10 $ 元的利润;而线上销售,需按销售额的 $ 20 \% $ 向平台支付管理费(其他额外成本忽略不计).若销售商第二批购进 $ 1500 $ kg 福橘,为了使全部售出后的总利润达到 $ 4700 $ 元,则实体店和线上应各售出多少盒?

答案： 解:
(1)设线上售出x盒,则实体店售出(x-40)盒.根据题意,得5x+3(x-40)=1000,解得x=140.
∴x-40=140-40=100.
答:实体店售出100盒,线上售出140盒.
(2)设线上售出y盒,则实体店售出$\frac{1500-5y}{3}$盒.由题意,得(50-25)y-50y·20%+10×$\frac{1500-5y}{3}$=4700,解得y=180.
∴$\frac{1500-5y}{3}$=$\frac{1500-5×180}{3}$=200.
答:实体店售出200盒,线上售出180盒.

11. 新考向 情境素材(2024·福州一中期末)如图,商品条形码是商品的“身份证”,共有 $ 13 $ 位数字.它是由前 $ 12 $ 位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码和校验码”.

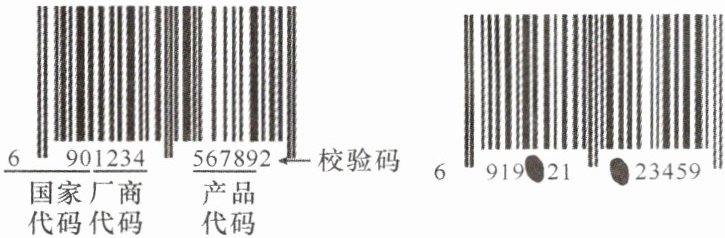
其中,校验码是用来校验商品条形码中前 $ 12 $ 位数字代码的正确性.它的编制是按照特定的算法得来的.其算法如下:
步骤 $ 1 $:计算前 $ 12 $ 位数字中偶数位数字的和 $ a $,即 $ a = 9 + 1 + 3 + 5 + 7 + 9 = 34 $;
步骤 $ 2 $:计算前 $ 12 $ 位数字中奇数位数字的和 $ b $,即 $ b = 6 + 0 + 2 + 4 + 6 + 8 = 26 $;
步骤 $ 3 $:计算 $ 3 a $ 与 $ b $ 的和 $ c $,即 $ c = 3 × 34 + 26 = 128 $;
步骤 $ 4 $:取大于或等于 $ c $ 且为 $ 10 $ 的整数倍的最小数 $ d $,即 $ d = 130 $;
步骤 $ 5 $:计算 $ d $ 与 $ c $ 的差就是校验码 $ x $,即 $ x = 130 - 128 = 2 $.
如图,若条形码中被污染的两个数字的和是 $ 7 $,则被污染的两个数字中右边的数字是3.

答案： 3