第130页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
7. 计算:
(1)$37^{\circ}49'+44^{\circ}28'$.
(2)$108^{\circ}18'-56.5^{\circ}$.
(1)$37^{\circ}49'+44^{\circ}28'$.
(2)$108^{\circ}18'-56.5^{\circ}$.
答案:
7.解:
(1)原式=81°77′=82°17′.
(2)原式=108°18′-56°30′=107°78′-56°30′=51°48′.
(1)原式=81°77′=82°17′.
(2)原式=108°18′-56°30′=107°78′-56°30′=51°48′.
8. (教材P178习题T9变式)已知$∠AOB=70^{\circ}$,以$OB$为边画$∠BOC=40^{\circ}$,则$∠AOC$的度数为
30°或110°
.
答案:
8.30°或110°
9. 如图,如果$∠CAE>∠BAD$,那么下列说法中一定正确的是(
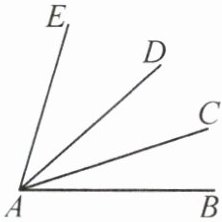
A.$∠BAC>∠CAD$
B.$∠DAE>∠CAD$
C.$∠CAE<∠BAC+∠DAE$
D.$∠BAC<∠DAE$
]
D
)
A.$∠BAC>∠CAD$
B.$∠DAE>∠CAD$
C.$∠CAE<∠BAC+∠DAE$
D.$∠BAC<∠DAE$
]
答案:
9.D
10. (教材P173“探究”变式)下列角度中,不能用一副三角板画出来的是(
A.$15^{\circ}$
B.$105^{\circ}$
C.$125^{\circ}$
D.$165^{\circ}$
C
)A.$15^{\circ}$
B.$105^{\circ}$
C.$125^{\circ}$
D.$165^{\circ}$
答案:
10.C
11. 如图,甲从点$A$出发向北偏东$69^{\circ}30'$方向走到点$B$,乙从点$A$出发向南偏西$18^{\circ}40'$方向走到点$C$,则$∠BAC$的度数是
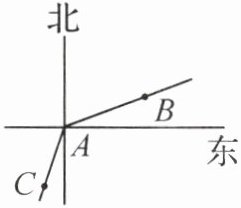
129°10′
.
答案:
11.129°10′
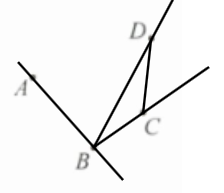
12. 如图,在同一平面内有四个点$A$,$B$,$C$,$D$.
(1)按要求补充图形:画出直线$AB$、射线$BC$、射线$BD$,连接$DC$.
(2)若小明在(1)的基础上测量$∠ABD=61^{\circ}42'15''$,$∠CBD=15^{\circ}30'$,求$∠ABC$的度数.
(3)若在(1)(2)的基础上,小亮又测量$∠BDC=15.5^{\circ}$,比较$∠BDC$与$∠CBD$的大小.
 ]
]
(1)按要求补充图形:画出直线$AB$、射线$BC$、射线$BD$,连接$DC$.
(2)若小明在(1)的基础上测量$∠ABD=61^{\circ}42'15''$,$∠CBD=15^{\circ}30'$,求$∠ABC$的度数.
(3)若在(1)(2)的基础上,小亮又测量$∠BDC=15.5^{\circ}$,比较$∠BDC$与$∠CBD$的大小.
 ]
]
答案:
12.解:
(1)
(2)
∵∠ABD=61°42′15″,∠CBD=15°30′,
∴∠ABC=∠ABD+∠CBD=61°42′15″+15°30′=77°12′15″.
(3)
∵∠CBD=15°30′=15.5°,∠BDC=15.5°,
∴∠BDC=∠CBD.
12.解:
(1)

(2)
∵∠ABD=61°42′15″,∠CBD=15°30′,
∴∠ABC=∠ABD+∠CBD=61°42′15″+15°30′=77°12′15″.
(3)
∵∠CBD=15°30′=15.5°,∠BDC=15.5°,
∴∠BDC=∠CBD.
13. 如图,将三个形状、大小完全一样的正方形的一个顶点重合放置,$∠FAG=45^{\circ}$,$∠BAC=30^{\circ}$,求$∠DAE$的度数.
 ]
]
 ]
]
答案:
13.解:由题意可得,∠FAC=∠GAD=∠EAB=90°,
∴∠DAF=∠GAD-∠FAG=90°-45°=45°,∠EAC=∠EAB-∠BAC=90°-30°=60°.
∵∠DAF-∠DAE+∠EAC=∠FAC,
∴∠DAE=∠DAF+∠EAC-∠FAC=45°+60°-90°=15°.
∴∠DAF=∠GAD-∠FAG=90°-45°=45°,∠EAC=∠EAB-∠BAC=90°-30°=60°.
∵∠DAF-∠DAE+∠EAC=∠FAC,
∴∠DAE=∠DAF+∠EAC-∠FAC=45°+60°-90°=15°.
查看更多完整答案,请扫码查看


