第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
11. (2024·福州三牧中学期中)若$|-m|=|-\dfrac{1}{2}|$,则 m 的值为(
A.±2
B.$-\dfrac{1}{2}$或$\dfrac{1}{2}$
C.$\dfrac{1}{2}$
D.$-\dfrac{1}{2}$
B
)A.±2
B.$-\dfrac{1}{2}$或$\dfrac{1}{2}$
C.$\dfrac{1}{2}$
D.$-\dfrac{1}{2}$
答案:
B
12. (2024·福州长乐区期中)如果$|a|=-a$成立,那么 a 可以是
−1(答案不唯一)
.(写出一个有理数)
答案:
−1(答案不唯一)
13. (2024·福州延安中学期中)下列四个数中,比-3 小的数是(
A.3
B.0
C.-5
D.$-\dfrac{1}{3}$
C
)A.3
B.0
C.-5
D.$-\dfrac{1}{3}$
答案:
C
14. (2024·福州长乐区期中)已知冰箱的冷冻温度要求为-18℃~-4℃,则下列温度符合要求的是(
A.-20℃
B.0℃
C.-8℃
D.5℃
C
)A.-20℃
B.0℃
C.-8℃
D.5℃
答案:
C
15. (2023·福州晋安区期末)如图所示,若数轴上的点 A,B 分别与有理数 a,b 对应,则下列关系正确的是(
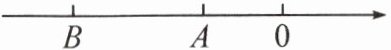
A.$a < b$
B.$-a > b$
C.$|a| > |b|$
D.$-a > -b$
B
)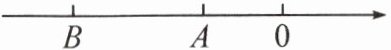
A.$a < b$
B.$-a > b$
C.$|a| > |b|$
D.$-a > -b$
答案:
B
16. (2024·厦门双十中学月考)已知有理数 a,b,其中数 a 在如图所示的数轴上对应点 M,b 是负数,且 b 在数轴上对应的点与原点的距离为 3.5.
(1)写出大于 b 的所有负整数.
(2)在数轴上标出表示$-\dfrac{1}{2}$,0,-2,b 的点,并用“<”连接起来.
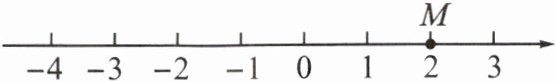
(1)写出大于 b 的所有负整数.
(2)在数轴上标出表示$-\dfrac{1}{2}$,0,-2,b 的点,并用“<”连接起来.
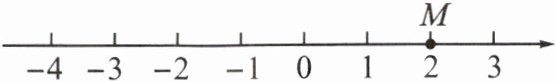
答案:
(1)
∵b是负数,且b在数轴上对应的点与原点的距离为3.5,
∴b对应的数是−3.5.
∴大于b的所有负整数为−3,−2,−1.
(2)如图所示,各点即为所求.

∴−3.5<−2<−$\frac{1}{2}$<0.
(1)
∵b是负数,且b在数轴上对应的点与原点的距离为3.5,
∴b对应的数是−3.5.
∴大于b的所有负整数为−3,−2,−1.
(2)如图所示,各点即为所求.

∴−3.5<−2<−$\frac{1}{2}$<0.
17. (2024·福州长乐区期中)1700 多年前,我国数学家刘徽首次明确地提出了正数和负数的概念. 他还规定筹算时“正算赤,负算黑”,即用红色算筹表示正数,黑色算筹表示负数. 例如:
(红色算筹) +34
(黑色算筹) -25
这个记载比国外早了差不多八百年. 根据上述材料,解决问题:

(1)如图,黑色算筹 表示的有理数是
表示的有理数是
(2)下列选项所示的算筹,表示-35 的是(

(3)请画算筹表示下列数:-14,+23,-(-4),-|-2|.
(红色算筹) +34
(黑色算筹) -25
这个记载比国外早了差不多八百年. 根据上述材料,解决问题:

(1)如图,黑色算筹
 表示的有理数是
表示的有理数是−23
.(2)下列选项所示的算筹,表示-35 的是(
A
)
(3)请画算筹表示下列数:-14,+23,-(-4),-|-2|.
答案:
(1)−23
(2)A
(3)−(−4)=4,−∣−2∣=−2.
∴用算筹表示−14,+23,−(−4),−∣−2∣如图:

(1)−23
(2)A
(3)−(−4)=4,−∣−2∣=−2.
∴用算筹表示−14,+23,−(−4),−∣−2∣如图:

查看更多完整答案,请扫码查看


