第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
9. 写出绝对值大于 $5$ 且小于 $8$ 的所有整数:
±6,±7
.
答案:
±6,±7
10. 下列说法中正确的是(
A.有理数中存在最大的数
B.任何数都大于它的相反数
C.最小的正整数是 $1$
D.两个数中,较大的那个数的绝对值也较大
C
)A.有理数中存在最大的数
B.任何数都大于它的相反数
C.最小的正整数是 $1$
D.两个数中,较大的那个数的绝对值也较大
答案:
C
11. 已知有理数 $a,b$ 在数轴上的对应点的位置如图所示,下列结论错误的是(
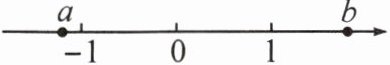
A.$-b < a < -1$
B.$1 < -a < b$
C.$1 < |a| < b$
D.$|a| < 1 < |b|$
D
)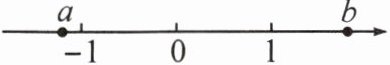
A.$-b < a < -1$
B.$1 < -a < b$
C.$1 < |a| < b$
D.$|a| < 1 < |b|$
答案:
D
12. 设 $[x)$ 表示小于 $x$ 的最大整数,如:$[-2.3) = -3,[4) = 3$. 则:
(1)$[5\frac{1}{2}) =$
(2)$[-3) =$
(3)$[-8\frac{1}{3}) =$
(1)$[5\frac{1}{2}) =$
5
.(2)$[-3) =$
−4
.(3)$[-8\frac{1}{3}) =$
−9
.
答案:
(1)5
(2)−4
(3)−9
(1)5
(2)−4
(3)−9
13. 已知在数轴上有 $A,B,C$ 三个点,点 $A$ 表示的数是 $-4$,点 $B$ 表示绝对值最小的数,点 $C$ 表示的数是最大的负整数.
(1)在数轴上把 $A,B,C$ 三点表示出来,并比较这三个点表示的数的大小(用“$<$”连接).
(2)直接写出如何移动点 $C$,可以使它到点 $A$ 和点 $B$ 的距离相等.
(1)在数轴上把 $A,B,C$ 三点表示出来,并比较这三个点表示的数的大小(用“$<$”连接).
(2)直接写出如何移动点 $C$,可以使它到点 $A$ 和点 $B$ 的距离相等.
答案:
(1)
∵点B表示绝对值最小的数,点C表示的数是最大的负整数,
∴点B表示的数是0,点C表示的数是−1.A,B,C三点在数轴上表示如图所示:(图略)根据数轴上左边的数小于右边的数可知,$-4 < -1 < 0$.
(2)将点C向左移动1个单位长度,可以使它到点A和点B的距离相等.
(1)
∵点B表示绝对值最小的数,点C表示的数是最大的负整数,
∴点B表示的数是0,点C表示的数是−1.A,B,C三点在数轴上表示如图所示:(图略)根据数轴上左边的数小于右边的数可知,$-4 < -1 < 0$.
(2)将点C向左移动1个单位长度,可以使它到点A和点B的距离相等.
14. 有理数 $a,b,c$ 在数轴上对应点的位置如图所示.

(1)用“$<$”“$>$”或“$=$”填空:$a$
(2)利用数轴化简:
① $|a| =$
② $|b| =$
③ $|c| =$
④ $|-a| =$
⑤ $|-b| =$
⑥ $|-c| =$
(3)在数轴上标出表示 $-a,-b,-c$ 的点,并将 $a,b,c,-a,-b,-c,0$ 用“$<$”连接起来.

(1)用“$<$”“$>$”或“$=$”填空:$a$
<
$0$,$b$<
$0$,$c$>
$0$.(2)利用数轴化简:
① $|a| =$
−a
.② $|b| =$
−b
.③ $|c| =$
c
.④ $|-a| =$
−a
.⑤ $|-b| =$
−b
.⑥ $|-c| =$
c
.(3)在数轴上标出表示 $-a,-b,-c$ 的点,并将 $a,b,c,-a,-b,-c,0$ 用“$<$”连接起来.
答案:
(1)< < >
(2)①−a ②−b ③c ④−a ⑤−b ⑥c
(3)图略,$b < a < -c < 0 < c < -a < -b$.
(1)< < >
(2)①−a ②−b ③c ④−a ⑤−b ⑥c
(3)图略,$b < a < -c < 0 < c < -a < -b$.
查看更多完整答案,请扫码查看


