《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

7. 图1是一种利用镜面反射放大微小变化的装置.在木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知AB⊥BC,MN⊥BC,AB= 6.5,BP= 4,PD= 8.
(1)ED的长为______.
(2)将木条BC绕点B按顺时针方向旋转一定角度得到BC'(如图2),点P的对应点为P',BC'与MN的交点为D',从A点发出的光束经平面镜P'反射后,在MN上的光点为E'.若DD'= 5,求EE'的长.

答案：

(1)13
(2)如图,过点E'作∠E'FD'=∠E'D'F,过点E'作E'G⊥BC于点G.
∴E'F=E'D',FG=GD'.
∵AB//MN,
∴∠ABD'+∠E'D'B=180°,
∴∠ABD'+∠E'FG=180°.
∵∠E'FB+∠E'FG=180°,
∴∠ABP'=∠E'FP'.
又∠AP'B=∠E'P'F,
∴△ABP'∽△E'FP',
∴$\frac{AB}{E'F}$=$\frac{BP'}{P'F}$,即$\frac{6.5}{E'F}$=$\frac{4}{P'F}$.
设P'F=4a,则E'F=6.5a,
∴E'D'=6.5a.
在Rt△BDD'中,∠BDD'=90°,DD'=5,BD=BP +PD=12,
由勾股定理可得,BD'=13,
∴cos∠BD'D=$\frac{5}{13}$.
在Rt△E'GD'中,cos∠BD'D=$\frac{GD'}{E'D'}$=$\frac{5}{13}$,
∴GD'=2.5a,
∴FG=GD'=2.5a.
∵BP'+P'F+FG+GD'=13,
∴4+4a+2.5a+2.5a=13,解得a=1,
∴E'D'=6.5,
∴EE'=DE+DD'-D'E'=13+5 - 6.5=11.5.

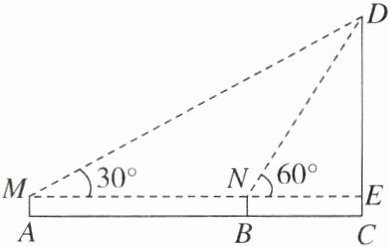
8. 小明利用所学三角函数知识对小区洋房的高度进行测量.他们在地面的A点处用测角仪测得楼房顶端D点的仰角为30°,向楼房前行20 m在B点处测得楼房顶端D点的仰角为60°,已知测角仪的高度是1.6 m(点A,B,C在同一条直线上),根据以上数据求楼房CD的高度.(参考数据：$\sqrt{3}\approx1.73$,结果取整数)

答案： 解:由题意得AM=BN=CE=1.6m,AB=MN=20m,∠DEM=90°,∠DNE=60°,∠DME=30°.
∵∠DNE是△DMN的外角,
∴∠MDN=∠DNE - ∠DMN=30°,
∴∠DMN=∠MDN=30°,
∴DN=MN=20m.
在Rt△DNE中,DE=DN·sin 60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(m),
∴DC=DE+CE=10$\sqrt{3}$+1.6≈17.3+1.6≈19(m).
答:楼房CD的高度约为19m.