《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

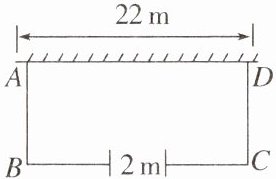
【例8】如图,要建一个矩形仓库ABCD,一边靠墙(墙长22m),并在BC边上开一道2m宽的门,现在可用的材料为38m长的木板.
(1)若仓库的面积为$150m^2,$求AB的长.
(2)当仓库的面积最大时,求AB的长,并指出仓库的最大面积.

答案： 解:
(1)设AB的长为x m,则AD=(38+2-2x)m,根据题意得,x(38+2-2x)=150,
解得$ x_{1}=15 $,$ x_{2}=5 $.
当$ x_{1}=15 $时,AD=10,当$ x_{2}=5 $时,AD=30＞22(不合题意,舍去),
∴AB=15 m.
(2)设仓库的面积为$ y\ m^2 $,
根据题意得,
$ y=x(38+2-2x)=-2x^2+40x=-2(x-10)^2+200 $,
∵a=-2＜0,38+2-2×10=20＜22,
∴当x=10时,$ y_{最大值}=200 $,
答:当AB=10 m时,仓库的最大面积为200 $ m^2 $.

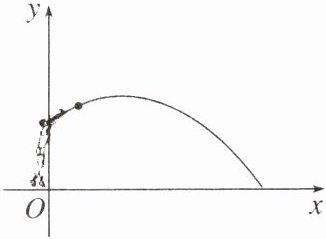
【变式】在体育课上,男生进行实心球投掷训练,实心球离手后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从实心球抛出到落地的过程中,实心球的竖直高度y(m)与水平距离x(m)近似满足函数关系$y= a(x-h)^{2}+k(a＜0)$.
(1)小强进行训练时,抛实心球的水平距离x与竖直高度y的几组数据如下：

根据上述数据,直接写出小强抛出实心球竖直高度的最大值,并求出满足的函数关系$y= a(x-h)^{2}+k(a＜0)$.
(2)小强改变了抛掷姿势,经多次训练后,实心球抛出的竖直高度y与水平距离x近似满足函数关系$y= ax^{2}+0.68x+1.7$.已知中考实心球的成绩满分标准是抛掷着陆时的水平距离至少为10m,若小强要获得满分,求a的取值范围.

答案： 解:
(1)根据表格中的数据可知,抛物线的顶点坐标为(3,2.6).
∴实心球竖直高度的最大值是2.6 m,
∴抛物线的函数关系式为$ y=a(x-3)^2+2.6 $,
把(0,1.7)代入关系式,得9a+2.6=1.7,
解得a=-0.1,
∴抛物线的函数关系式为$ y=-0.1(x-3)^2+2.6 $.
(2)当着陆时的水平距离为10 m时,即x=10,y=0,则100a+6.8+1.7=0,解得a=-0.085.
∵抛掷着陆时的水平距离越大,说明抛物线开口越大,
∴抛掷着陆时的水平距离大于10 m时,$|a|＜|-0.085|$,
∴$ a＞-0.085 $,
∴若抛掷着陆时的水平距离至少为10 m,则a的取值范围是$ -0.085＜a＜0 $.

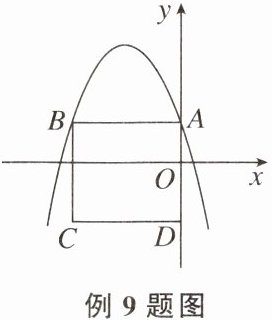
【例9】如图,在平面直角坐标系中,点A是抛物线$y= a(x+\frac{3}{2})^{2}+k(a≠0)$与y轴的交点,点B是这条抛物线上的另一点,且$AB// x$轴,则以AB为边的正方形ABCD的周长为12.

答案： 12

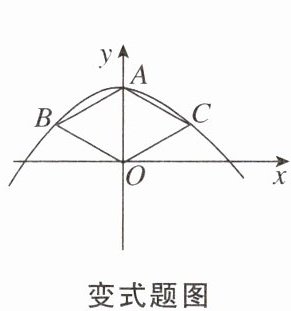
【变式】如图,在平面直角坐标系中,二次函数$y= ax^{2}+c(a＜0)$的图象过菱形ABOC的三个顶点A,B,C,$\angle BAC= 120^{\circ}$,则ac的值是$ -\frac{2}{3} $.

答案： $ -\frac{2}{3} $