第57页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
【例5】如图,A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE= 4,CD= 6,则AE的长为

5
.
答案:
5
【变式】如图,在Rt△ABC中,∠ABC= 90°,AB= 3,BC= 4.在Rt△MPN中,∠MPN= 90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE= 2PF时,AP=
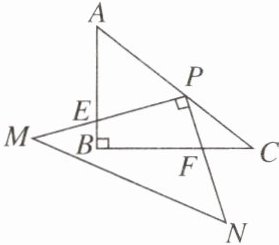
3
.
答案:
3
1. 下列条件不能判定△ADB∽△ABC的是(
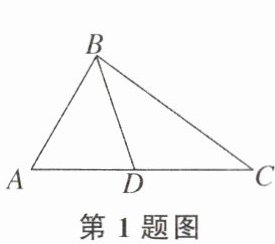
A.∠ABD= ∠ACB
B.∠ADB= ∠ABC
C.$\frac{AD}{AC}= \frac{DB}{BC}$
D.$AB^2= AD\cdot AC$
C
)
A.∠ABD= ∠ACB
B.∠ADB= ∠ABC
C.$\frac{AD}{AC}= \frac{DB}{BC}$
D.$AB^2= AD\cdot AC$
答案:
C
2. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC= 3:1,连结AE交BD于点F,则△DEF的面积与△BAF的面积之比为(
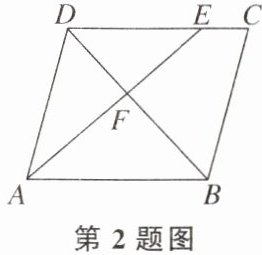
A.3:4
B.3:1
C.9:1
D.9:16
D
)
A.3:4
B.3:1
C.9:1
D.9:16
答案:
D
3. 如图,在△ABC中,点D在BC边上,连结AD,点G在线段AD上,GE//BD,且交AB于点E,GF//AC,且交CD于点F,则下列结论中一定正确的是(
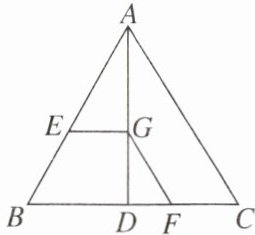
A.$\frac{AB}{AE}= \frac{AG}{AD}$
B.$\frac{DF}{CF}= \frac{DG}{AD}$
C.$\frac{FG}{AC}= \frac{EG}{BD}$
D.$\frac{AE}{BE}= \frac{CF}{DF}$
D
)
A.$\frac{AB}{AE}= \frac{AG}{AD}$
B.$\frac{DF}{CF}= \frac{DG}{AD}$
C.$\frac{FG}{AC}= \frac{EG}{BD}$
D.$\frac{AE}{BE}= \frac{CF}{DF}$
答案:
D
4. 如图,AB是半圆O的直径,点D是AB上任意一点(不与点A,B重合),作CD⊥AB与半圆交于点C,设AD= a,BD= b,则$\frac{a+b}{2}$______$\sqrt{ab}$.(填“>”“<”“≥”或“≤”)
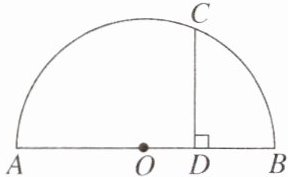

答案:
≥ [解析]连结AC,BC,OC,如图.
∵AB为半圆O的直径,AB=AD+BD=a+b,
∴∠ACB=90°,OC= $\frac{a+b}{2}$,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴$\frac{CD}{BD}$ = $\frac{AD}{CD}$,即$\frac{CD}{b}$ = $\frac{a}{CD}$,
∴CD= $\sqrt{ab}$.
∵OC≥CD(当点C平分$\overset{\frown}{AB}$时取等号),
∴$\frac{a+b}{2}$≥$\sqrt{ab}$.

≥ [解析]连结AC,BC,OC,如图.
∵AB为半圆O的直径,AB=AD+BD=a+b,
∴∠ACB=90°,OC= $\frac{a+b}{2}$,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴$\frac{CD}{BD}$ = $\frac{AD}{CD}$,即$\frac{CD}{b}$ = $\frac{a}{CD}$,
∴CD= $\sqrt{ab}$.
∵OC≥CD(当点C平分$\overset{\frown}{AB}$时取等号),
∴$\frac{a+b}{2}$≥$\sqrt{ab}$.

5. 如图,直线DE分别交AC,AB于点D,F,交CB的延长线于点E,且BE:BC= 2:3,AD= CD,求AF:BF的值.
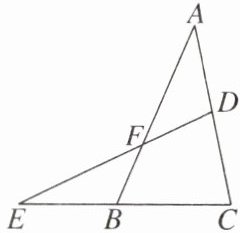

答案:
解:如图,过点D作DG//AB交BC于点G.
又
∵AD=CD,
∴DG=$\frac{1}{2}$AB,BG=GC,

∵BE:BC=2:3,
∴BE:BG=2:1.5=4:3.
易知△EBF∽△EGD,
∴$\frac{BF}{GD}$=$\frac{EB}{EG}$=$\frac{4}{7}$
∴$\frac{BF}{AB}$=$\frac{4}{14}$=$\frac{2}{7}$,
∴AF:BF=5:2.
解:如图,过点D作DG//AB交BC于点G.
又
∵AD=CD,
∴DG=$\frac{1}{2}$AB,BG=GC,

∵BE:BC=2:3,
∴BE:BG=2:1.5=4:3.
易知△EBF∽△EGD,
∴$\frac{BF}{GD}$=$\frac{EB}{EG}$=$\frac{4}{7}$
∴$\frac{BF}{AB}$=$\frac{4}{14}$=$\frac{2}{7}$,
∴AF:BF=5:2.
查看更多完整答案,请扫码查看


