第54页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 如果两个三角形相似,相似比为 4:9,那么这两个三角形的 (
A.周长之比为 2:3
B.周长之比为 4:9
C.面积之比为 2:3
D.面积之比为 4:9
B
)A.周长之比为 2:3
B.周长之比为 4:9
C.面积之比为 2:3
D.面积之比为 4:9
答案:
B
2. 如图,△ABC 与△DEF 都是正方形网格中的格点三角形(顶点在格点上),则△ABC 与△DEF 的面积比是 (
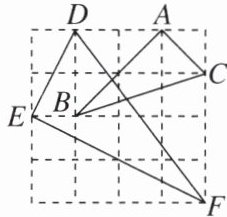
A.1:2
B.2:5
C.$\sqrt{2}:\sqrt{5}$
D.1:3
B
) 
A.1:2
B.2:5
C.$\sqrt{2}:\sqrt{5}$
D.1:3
答案:
B
3. 若两个相似三角形的面积比是 16:9,则这两个三角形对应边上的高之比是 (
A.16:9
B.9:16
C.3:4
D.4:3
D
)A.16:9
B.9:16
C.3:4
D.4:3
答案:
D
4. 已知△ABC∽△DEF,AB:DE= 1:$\sqrt{2}$,则△DEF 与△ABC 面积的比为 (
A.2:1
B.1:4
C.1:2
D.4:1
A
)A.2:1
B.1:4
C.1:2
D.4:1
答案:
A
5. 有一个直角三角形的边长分别为 3,4,5,另一个与它相似的直角三角形的最小边长为 7,则另一个直角三角形的周长是 (
A.$\frac{42}{5}$
B.$\frac{84}{5}$
C.21
D.28
D
)A.$\frac{42}{5}$
B.$\frac{84}{5}$
C.21
D.28
答案:
D
6. 如果两个相似三角形的对应中线之比是 1:4,那么它们的周长之比是
1∶4
.
答案:
1∶4
7. 如图,在△ABC 中,D,E 分别是边 AB,AC 上的点,且 DE//BC,若△ADE 与△ABC 的周长之比为 2:3,AD= 4,则 DB=
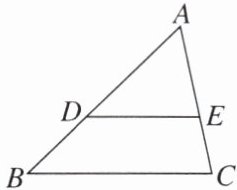
2
.
答案:
2
8. 如图,AB 与 CD 相交于点 O,△OBD∽△OAC,$\frac{OD}{OC}= \frac{3}{5}$,OB= 6,$S_{\triangle AOC}= 50$,求:
(1)AO 的长.
(2)$S_{\triangle BOD}$的值.

(1)AO 的长.
(2)$S_{\triangle BOD}$的值.

答案:
解:
(1)
∵△OBD∽△OAC,
∴$\frac{BO}{AO}=\frac{DO}{CO}=\frac{3}{5}$.
∵BO=6,
∴AO=10.
(2)
∵△OBD∽△OAC,$\frac{OD}{OC}=\frac{3}{5}$,
∴$\frac{S_{\triangle BOD}}{S_{\triangle AOC}}=\frac{9}{25}$.
∵$S_{\triangle AOC}=50$,
∴$S_{\triangle BOD}=18$.
(1)
∵△OBD∽△OAC,
∴$\frac{BO}{AO}=\frac{DO}{CO}=\frac{3}{5}$.
∵BO=6,
∴AO=10.
(2)
∵△OBD∽△OAC,$\frac{OD}{OC}=\frac{3}{5}$,
∴$\frac{S_{\triangle BOD}}{S_{\triangle AOC}}=\frac{9}{25}$.
∵$S_{\triangle AOC}=50$,
∴$S_{\triangle BOD}=18$.
查看更多完整答案,请扫码查看


