《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

【例3】如图,为了测量某条河的对岸C,D两点间的距离.在河的岸边与CD平行的直线EF上取两点A,B,测得∠BAC= 45°,∠ABC= 37°,∠DBF= 60°,量得AB的长为70米.求C,D两点间的距离.(参考数据：$\sin 37^\circ\approx\frac{3}{5}$,$\cos 37^\circ\approx\frac{4}{5}$,$\tan 37^\circ\approx\frac{3}{4}$)

答案：
解:如图,过点C,D分别作CM⊥EF,DN⊥EF,垂足分别为M,N.
在Rt△AMC中,
∵∠BAC=45°,
∴AM=MC.
在Rt△BMC中,
∵∠ABC=37°,tan∠ABC=$\frac{CM}{BM}$,
∴BM=$\frac{CM}{\tan37^\circ}$≈$\frac{4}{3}$CM.
∵AB=AM+BM≈CM+$\frac{4}{3}$CM=70米,
∴CM=DN≈30米.
在Rt△BDN中,
∵∠DBN=60°,
∴BN=$\frac{DN}{\tan60^\circ}$=$\frac{30}{\sqrt{3}}$=10$\sqrt{3}$(米),
∴CD=MN=MB+BN≈$\frac{4}{3}$×30+10$\sqrt{3}$=(40 +10$\sqrt{3}$)米.
答:C,D两点间的距离约为(40+10$\sqrt{3}$)米.

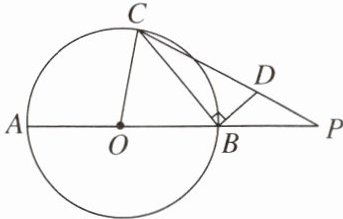
【变式】如图,AB是⊙O的直径,延长AB至点P,使BP= OB,BD垂直于弦BC,垂足为B,点D在PC上.设∠PCB= α,∠POC= β.求证：$\tan\alpha\tan\frac{\beta}{2}= \frac{1}{3}$.

答案：
证明:如图,连结AC,则∠A=$\frac{1}{2}$∠POC=$\frac{\beta}{2}$.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC.
∵BD⊥BC,
∴BD//AC,
∴∠PBD=∠A.
∵∠P=∠P,
∴△PBD∽△PAC,
∴$\frac{BD}{AC}$=$\frac{PB}{PA}$.
∵PB=OB=OA,
∴$\frac{PB}{PA}$=$\frac{1}{3}$,
∴$\frac{BD}{AC}$=$\frac{1}{3}$,
∴tanαtan$\frac{\beta}{2}$=$\frac{BD}{BC}$·$\frac{BC}{AC}$=$\frac{BD}{AC}$=$\frac{1}{3}$.

【例4】某地革命根据地纪念馆广场上屹立着三位革命家的塑像.某数学兴趣小组计划在假期前往该革命根据地学习,并测量塑像高度,活动方案如下：
测量方案：如图,点B,E,F,D四点在同一条直线上,在点E处放置平面镜,此时小明视线刚好在平面镜内看到塑像顶端C的像,在点F处安装测倾器,测得塑像顶端C的仰角约为51.3°.
数据收集：测得眼睛离地面的高度AB= 1.6米,BE= 2米,EF= 4米,GF= 1.4米,AB⊥BD,GF⊥BD,CD⊥BD.
解决问题：求塑像CD的高度.(结果精确到0.1米.参考数据：$\sin 51.3^\circ\approx0.78$,$\cos 51.3^\circ\approx0.63$,$\tan 51.3^\circ\approx1.25$)

答案：
解:过点G作GH⊥CD,垂足为H,如图.
由题意得,∠AEB=∠CED,FG=DH=1.4米.
设GH=DF=x米,
∵EF=4米,
∴DE=EF+DF=(x+4)米.
在Rt△CGH中,∠CGH=51.3°,
∴CH=GH·tan51.3°≈1.25x米,
∴CD=CH+DH=(1.25x+1.4)米.
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴△ABE∽△CDE.
∴$\frac{AB}{CD}$=$\frac{BE}{DE}$,
∴$\frac{1.6}{1.25x+1.4}$=$\frac{2}{x+4}$.解得x=4,
经检验,x=4是原方程的根,
∴CD=1.25x+1.4=6.4(米).
答:塑像CD的高度约为6.4米.